diff --git a/img/stapeldiagramm_countdown.svg b/img/stapeldiagramm_countdown.svg
index dae7863c13a5a6a80a735fd570d41395081b05e1..ae656d02e9191f080aa6f11e1b1f05e070bbb25b 100644
--- a/img/stapeldiagramm_countdown.svg
+++ b/img/stapeldiagramm_countdown.svg
@@ -9,13 +9,13 @@
xmlns="http://www.w3.org/2000/svg"
xmlns:sodipodi="http://sodipodi.sourceforge.net/DTD/sodipodi-0.dtd"
xmlns:inkscape="http://www.inkscape.org/namespaces/inkscape"
- width="210mm"
- height="297mm"
- viewBox="0 0 210 297"
+ width="43.481136mm"
+ height="46.042965mm"
+ viewBox="0 0 43.481136 46.042965"
version="1.1"
id="svg8"
inkscape:version="0.92.1 r15371"
- sodipodi:docname="stack_diagram_countdown.svg">
+ sodipodi:docname="stapeldiagramm_countdown.svg">
<defs
id="defs2" />
<sodipodi:namedview
@@ -25,17 +25,21 @@
borderopacity="1.0"
inkscape:pageopacity="0.0"
inkscape:pageshadow="2"
- inkscape:zoom="3.0227835"
- inkscape:cx="250.94239"
- inkscape:cy="966.01732"
+ inkscape:zoom="1.0687154"
+ inkscape:cx="-34.35743"
+ inkscape:cy="99.767279"
inkscape:document-units="mm"
inkscape:current-layer="layer1"
showgrid="false"
inkscape:window-width="1920"
- inkscape:window-height="1010"
+ inkscape:window-height="1009"
inkscape:window-x="0"
- inkscape:window-y="33"
- inkscape:window-maximized="1" />
+ inkscape:window-y="34"
+ inkscape:window-maximized="1"
+ fit-margin-top="0"
+ fit-margin-left="0"
+ fit-margin-right="0"
+ fit-margin-bottom="0" />
<metadata
id="metadata5">
<rdf:RDF>
@@ -44,14 +48,15 @@
<dc:format>image/svg+xml</dc:format>
<dc:type
rdf:resource="http://purl.org/dc/dcmitype/StillImage" />
- <dc:title />
+ <dc:title></dc:title>
</cc:Work>
</rdf:RDF>
</metadata>
<g
inkscape:label="Ebene 1"
inkscape:groupmode="layer"
- id="layer1">
+ id="layer1"
+ transform="translate(-18.941391,-22.111829)">
<text
xml:space="preserve"
style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:4.23333311px;line-height:100%;font-family:arial;-inkscape-font-specification:arial;text-align:center;letter-spacing:0px;word-spacing:0px;writing-mode:lr-tb;text-anchor:middle;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.26458332px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1"
diff --git a/notebooks/seminar04.ipynb b/notebooks/seminar04.ipynb
index 110baea107615a5377d3c455f9b49f720aedb17c..48ad7fdafffa132f6a16aac6faefc58f91e7e79e 100644
--- a/notebooks/seminar04.ipynb
+++ b/notebooks/seminar04.ipynb
@@ -612,7 +612,7 @@
"\n",
"#### Aufgabe 2\n",
"\n",
- "[Schildkröten-Blumen](http://greenteapress.com/thinkpython2/html/thinkpython2003.png)\n",
+ "\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Blumen.\n",
"\n",
@@ -620,7 +620,7 @@
"\n",
"#### Aufgabe 3\n",
"\n",
- "[Schildkröten-Kuchen](http://greenteapress.com/thinkpython2/html/thinkpython2004.png)\n",
+ "\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Figuren.\n",
"\n",
diff --git a/notebooks/seminar05.ipynb b/notebooks/seminar05.ipynb
index 9b444c49ca4d386c0fbc6b2b31dd3a910ab70be8..9e0e383ee2ebbaeb5f417bdf80ac66183961cb2d 100644
--- a/notebooks/seminar05.ipynb
+++ b/notebooks/seminar05.ipynb
@@ -27,7 +27,25 @@
" n = n // 2\n",
" return ergebnis\n",
"\n",
- "print(dez_zu_bin(42))"
+ "print(dez_zu_bin(42))\n",
+ "\n",
+ "# Und weil wir heute beim Thema Rekursion sind ...\n",
+ "def dez_zu_bin_rekursiv(n):\n",
+ " if n == 0:\n",
+ " return \"\"\n",
+ " return dez_zu_bin_rekursiv(n // 2) + str(n % 2)\n",
+ "\n",
+ "print(dez_zu_bin_rekursiv(42))\n",
+ "\n",
+ "def dez_zu_allem(n, s):\n",
+ " if n == 0:\n",
+ " return \"\"\n",
+ " return dez_zu_allem(n // len(s)) + s[n % len(s)]\n",
+ "\n",
+ "print(dez_zu_allem(42, \"01\"))\n",
+ "print(dez_zu_allem(42, \"0123456789\"))\n",
+ "print(dez_zu_allem(42, \"01234567\"))\n",
+ "print(dez_zu_allem(42, \"0123456789ABCDEF\"))"
]
},
{
@@ -499,7 +517,7 @@
"\n",
"([Tabletop Roleplaying](https://xkcd.com/244/), Randall Munroe)\n",
"\n",
- "Es ist erlaubt, dass eine Funktion eine andere aufruft; Es ist auch erlaubt, dass die Funktion sich selbst aufruft. Es ist vielleicht nicht offensichtlich, warum das eine gute Idee ist, aber es ist eines der \"magischsten\" Dinge, die ein Program tun kann. Schauen wir uns beispielsweise die folgende Funktion an:\n"
+ "Es ist erlaubt, dass eine Funktion eine andere aufruft; es ist auch erlaubt, dass die Funktion sich selbst aufruft. Es ist vielleicht nicht offensichtlich, warum das eine gute Idee ist, aber es ist eines der \"magischsten\" Dinge, die ein Program tun kann. Schauen wir uns beispielsweise die folgende Funktion an:\n"
]
},
{
@@ -599,11 +617,11 @@
"\n",
"Die folgende Abbildung zeigt ein Stapeldiagramm für den Aufruf von `countdown(3)`:\n",
"\n",
- "\n",
+ "\n",
"\n",
"Wie üblich, ist oben auf dem Stapel der Block für `__main__`. Dieser ist leer, denn wir haben in `main` keine Variablen erstellt oder Argumente übergeben.\n",
"\n",
- "Die vier Blöcke für `countdown` haben unterschiedliche Werte für den Parameter `n`. Der Block am Boden des Stapels, wo `n=0` ist, wird **Basisfall** genannt. In diesem gibt es keinen rekursiven Aufruf, daher gibt es keine weiteren Blöcke.\n",
+ "Die vier Blöcke für `countdown` haben unterschiedliche Werte für den Parameter `n`. Der Block am Boden des Stapels, wo `n=0` ist, wird **Basisfall** genannt. In diesem gibt es keinen rekursiven Aufruf, daher gibt es keine weiteren Blöcke. Dies ist gleichzeitig die **Abbruchbedingung** für die Rekursion.\n",
"\n",
"Zeichnen Sie als Übung ein Stapeldiagramm für `print_n`, wenn es mit `s = 'Hallo'` und `n = 2` aufgerufen wird. Schreiben Sie dann eine Funktion `do_n`, die ein Funktionsobjekt und eine ganze Zahl `n` als Parameter erwartet und dann die übergebene Funktion `n`-mal aufruft. \n"
]
@@ -647,7 +665,11 @@
"\n",
"Dieser Traceback ist etwas größer als der, den wir im vorherigen Kapitel gesehen haben. Wenn der Fehler auftritt, befinden sich 1000 `recurse`-Blöcke auf dem Stapel!\n",
"\n",
- "Wenn bei ihnen eine ungewollte unendliche Rekursion auftritt, überprüfen Sie Ihre Funktion und stellen Sie sicher, dass es einen Basisfall gibt, der keinen rekursiven Aufruf tätigt. Und wenn es einen Basisfall gibt, überprüfen Sie, ob er garantiert erreicht wird."
+ "Wenn bei ihnen eine ungewollte unendliche Rekursion auftritt, überprüfen Sie Ihre Funktion und stellen Sie sicher, dass es einen Basisfall gibt, der keinen rekursiven Aufruf tätigt. Und wenn es einen Basisfall gibt, überprüfen Sie, ob er garantiert erreicht wird.\n",
+ "\n",
+ "\n",
+ "\n",
+ "([Wolfgang Beyer ](https://commons.wikimedia.org/wiki/File:Mandel_zoom_07_satellite.jpg))"
]
},
{
@@ -692,7 +714,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Die Folge `\\n` am Ende des Hinweises repräsentiert einen **Zeilenumbruch** -- ein spezielles Zeichen, welches einen Zeilenumbruch bewirkt. Aus diesem Grund erscheint die Eingabe des Nutzers unter dem Hinweis.\n",
+ "Die Folge `\\n` am Ende des Hinweises repräsentiert einen **Zeilenumbruch** - ein spezielles Zeichen, welches einen Zeilenumbruch bewirkt. Aus diesem Grund erscheint die Eingabe des Nutzers unter dem Hinweis.\n",
"\n",
"Falls wir erwarten, dass der Nutzer eine ganze Zahl eintippt, können wir versuchen, die Eingabe in eine ganze Zahl umzuwandeln:"
]
@@ -703,7 +725,7 @@
"metadata": {},
"outputs": [],
"source": [
- "prompt = \"Wie hoch ist die Fluggeschwindigkeit einer unbeladeten Schwalbe?\\n\"\n",
+ "prompt = \"Wie hoch ist die Fluggeschwindigkeit einer unbeladenen Schwalbe?\\n\"\n",
"speed = input(prompt)\n",
"int(speed)"
]
@@ -721,6 +743,16 @@
"Wir werden später sehen, wie wir diese Art von Fehler behandeln können."
]
},
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from IPython.display import YouTubeVideo\n",
+ "YouTubeVideo('liIlW-ovx0Y')"
+ ]
+ },
{
"cell_type": "markdown",
"metadata": {},
@@ -858,13 +890,24 @@
"print_time()"
]
},
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "\n",
+ "\n",
+ "([2038](https://xkcd.com/607/), Randall Munroe)"
+ ]
+ },
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Aufgabe 2\n",
"\n",
- "[Fermats letzter Satz](https://de.wikipedia.org/wiki/Fermazs_letzter_Satz) besagt dass es keine positiven ganzen Zahlen $a$,$b$ und $c$ gibt, so dass\n",
+ "\n",
+ "\n",
+ "[Fermats letzter Satz](https://de.wikipedia.org/wiki/Gro%C3%9Fer_Fermatscher_Satz) besagt dass es keine positiven ganzen Zahlen $a$,$b$ und $c$ gibt, so dass\n",
"\\begin{equation}\n",
"a^n + b^n = c^n\n",
"\\end{equation}\n",
@@ -889,7 +932,7 @@
"source": [
"#### Aufgabe 3\n",
"\n",
- "Wenn uns drei Stöcke gegeben werden, kann es sein, dass wir sie als Dreieck anordnen können oder aber auch nicht. Wenn beispielsweise einer der Stöcke 12cm lang ist und die anderen beiden jeweils 1cm, dann klappt es nicht. Für jede Kombination von Längen gibt es einen einfachen Test, der uns anzeigt, ob sich daraus ein Dreieck formen lässt:\n",
+ "Wenn uns drei Stöcke gegeben werden, kann es sein, dass wir sie als Dreieck anordnen können oder auch nicht. Wenn beispielsweise einer der Stöcke 12cm lang ist und die anderen beiden jeweils 1cm, dann klappt es nicht. Für jede Kombination von Längen gibt es einen einfachen Test, der uns anzeigt, ob sich daraus ein Dreieck formen lässt:\n",
"\n",
"*Falls eine der drei Längen größer als die Summe der anderen beiden Längen ist, dann lässt sich kein Dreieck formen. (Wenn die Summe der beiden Längen gleich der dritten Länge ist, dann bilden Sie ein sogenanntes \"degeneriertes\" Dreieck.)*\n",
"\n",
@@ -946,7 +989,7 @@
"Die folgenden Aufgaben nutzen das `turtle`-Modul welches in [Kapitel 4](seminar04.ipynb) beschrieben wurde.\n",
"\n",
"#### Aufgabe 5\n",
- "Lesen Sie sich die folgende Funktion durch und versuchen Sie herauszufinden, was sie tut (schauen Sie sich auch die Beispiele in Kapitel 4 an). Rufen Sie erst dann die Funktion auf und schauen Sie, ob Sie richtig liegen."
+ "Lesen Sie sich die folgende Funktion durch und versuchen Sie herauszufinden, was sie tut (schauen Sie sich auch die [Beispiele in Kapitel 4](seminar04.ipynb#4.12-%C3%9Cbung) an). Rufen Sie erst dann die Funktion auf und schauen Sie, ob Sie richtig liegen."
]
},
{
@@ -972,29 +1015,35 @@
"cell_type": "markdown",
"metadata": {},
"source": [
+ "\n",
+ "\n",
"#### Aufgabe 6\n",
"\n",
- "Die [Kochkurve](https://de.wikipedia.org/wiki/Kochkurve) ist ein [Fraktal](https://de.wikipedia.org/wiki/Fraktal), welches ungefähr so aussieht:\n",
+ "Die [Koch-Kurve](https://de.wikipedia.org/wiki/Koch-Kurve) ist ein [Fraktal](https://de.wikipedia.org/wiki/Fraktal), welches ungefähr so aussieht:\n",
"\n",
"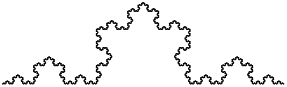\n",
"\n",
- "Um eine Kochkurve der Länge x zu zeichnen, müssen wir nur folgendes tun:\n",
+ "Um eine Koch-Kurve der Länge x zu zeichnen, müssen wir nur folgendes tun:\n",
"\n",
- "1. Eine Kochkurve der Länge x/3 zeichnen.\n",
+ "1. Eine Koch-Kurve der Länge x/3 zeichnen.\n",
"2. Um 60° nach links drehen.\n",
- "3. Eine Kochkurve der Länge x/3 zeichnen.\n",
+ "3. Eine Koch-Kurve der Länge x/3 zeichnen.\n",
"2. Um 120° nach rechts drehen.\n",
- "3. Eine Kochkurve der Länge x/3 zeichnen.\n",
+ "3. Eine Koch-Kurve der Länge x/3 zeichnen.\n",
"2. Um 60° nach links drehen.\n",
- "3. Eine Kochkurve der Länge x/3 zeichnen.\n",
+ "3. Eine Koch-Kurve der Länge x/3 zeichnen.\n",
"\n",
"Eine Ausnahme gibt es, falls x kleiner als 3 ist: dann zeichnen wir einfach eine Strecke der Länge 3.\n",
"\n",
- "1. Schreiben Sie eine Funktion `koch`, die eine Schildkröte und eine Länge als Argumente erwartet und die Schildkröte nutzt, um eine Kochkurve der gegebenen Länge zu zeichnen.\n",
- "2. Schreiben Sie eine Funktion `schneeflocke`, die drei Kochkurven zeichnet, so dass sich der Umriss einer Schneeflocke ergibt.\n",
+ "1. Schreiben Sie eine Funktion `koch`, die eine Schildkröte und eine Länge als Argumente erwartet und die Schildkröte nutzt, um eine Koch-Kurve der gegebenen Länge zu zeichnen.\n",
+ "2. Schreiben Sie eine Funktion `schneeflocke`, die drei Koch-Kurven zeichnet, so dass sich der Umriss einer Schneeflocke ergibt.\n",
"\n",
" Lösung: http://thinkpython2.com/code/koch.py\n",
- "3. Die Kochkurve kann auf verschiedene Art und Wiese verallgemeinert werden. Schauen Sie sich die Beispiele auf http://en.wikipedia.org/wiki/Koch_snowflake an und implementieren Sie ihren Favoriten."
+ "3. Die Koch-Kurve kann auf verschiedene Art und Wiese verallgemeinert werden. Schauen Sie sich die [Beispiele auf Wikipedia](https://en.wikipedia.org/wiki/Koch_snowflake#Variants_of_the_Koch_curve) an und implementieren Sie ihren Favoriten.\n",
+ "\n",
+ "\n",
+ "\n",
+ "([Eric Baird](https://commons.wikimedia.org/wiki/File:Koch_Curve_in_Three_Dimensions_%28%22Delta%22_fractal%29.jpg))"
]
},
{
@@ -1008,9 +1057,9 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "\n",
+ "\n",
"\n",
- "Herzlichen Glückwunsch! Sie haben das 4. Kapitel geschafft. Weiter geht es in [5: Bedingungen und Rekursion](seminar05.ipynb)."
+ "Herzlichen Glückwunsch! Sie haben das 5. Kapitel geschafft. Weiter geht es in [6: Ergebnisreiche Funktionen](seminar06.ipynb)."
]
}
],