diff --git a/notebooks/seminar04.ipynb b/notebooks/seminar04.ipynb
index 2560eae592c0413589daed0a4e2595481dcb9789..08fc844059880e4e4ed36ae139e7108525a93ff4 100644
--- a/notebooks/seminar04.ipynb
+++ b/notebooks/seminar04.ipynb
@@ -6,7 +6,14 @@
    "source": [
     "# Seminar Problemorientierte Programmierung\n",
     "\n",
-    "## Ihre Lernziele\n",
+    "## 4: Fallstudie: Schnittstellenentwurf\n",
+    "[Chapter 4: Case Study: interface design](http://greenteapress.com/thinkpython/html/thinkpython005.html)\n",
+    "\n",
+    "In diesem Kapitel lernen wir, anhand einer Fallstudie, wie wir Funktionen entwerfen können, die gut zusammenarbeiten.\n",
+    "\n",
+    "Wir lernen außerdem das `turtle`-Modul kennen, mit dessen Hilfe wir Graphiken erzeugen können.\n",
+    "\n",
+    "### Ihre Lernziele\n",
     "\n",
     "Beschreiben Sie in 2-3 Stichpunkten kurz was Sie im Seminar heute lernen wollen. Klicken Sie dazu doppelt auf diesen Text und bearbeiten Sie dann den Text:\n",
     "\n",
@@ -15,9 +22,7 @@
     "- \n",
     "\n",
     "\n",
-    "## Exkurs: Was mir an Python gefällt\n",
-    "\n",
-    "In dieser Rubrik, die immer am Anfang eines Kapitels steht, möchte ich Ihnen zeigen, wofür ich Python nutze und warum ich es mag. Sie werden vielleicht noch nicht verstehen, was ich genau mache, aber Sie sehen damit schon einmal die Möglichkeiten von Python und können später darauf zurückgreifen. Da dies auch ein Exkurs ist, können Sie diese Rubrik gerne auch erst einmal überspringen.\n",
+    "### Exkurs: Was mir an Python gefällt\n",
     "\n",
     "Man kann schnell und einfach ein Programm aufschreiben und testen. Man muss es weder kompilieren, noch viel \"unnötige\" Syntax kennen:"
    ]
@@ -41,12 +46,44 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 4: Fallstudie: Schnittstellenentwurf\n",
-    "\n",
-    "In diesem Kapitel lernen wir anhand einer Fallstudie, wie wir Funktionen entwerfen können, die gut zusammenarbeiten.\n",
-    "\n",
-    "Wir lernen außerdem das `turtle`-Modul kennen, mit dessen Hilfe wir Graphiken erzeugen können. \n",
-    "\n",
+    "### 4.0 Python für das `turtle`-Modul\n",
+    "\n",
+    "Da das `turtle`-Modul in Jupyter-Notebooks eventuell nicht so gut funktioniert, kann es von Vorteil sein, `turtle` über die Kommandozeile aufzurufen. Dies ist prinzipell auf allen Betriebssystemen möglich, aber auf Linux und MacOS deutlich einfacher als auf Windows.\n",
+    "\n",
+    "Falls Sie Linux nutzen, sollte Python bereits installiert sein. Um das gewünschte Programm zu öffnen tuen Sie folgendes: \n",
+    "1. Speichern Sie das Programm, das sie aufrufen möchten als Python Programm (.py)\n",
+    "2. Öffnen Sie die Kommandozeile\n",
+    "3. Gehen Sie entweder in das Verzeichnis, in dem das Programm gespeichert ist, dafür geben Sie `cd /pfad/zum/verzeichnis`  ein. \n",
+    "4. Geben Sie auf der Kommandozeile `python programm.py` ein\n",
+    "5. Alternativ können Sie auch `python /pfad/zum/verzeichnis/programm.py` eingeben. \n",
+    "\n",
+    "Falls Sie MacOS verwenden, gehen Sie folgendermaßen vor:\n",
+    "1. Speichern Sie das Programm, dass Sie aufrufen möchten als Python Programm (.py)\n",
+    "2. Öffnen Sie das Terminal\n",
+    "3. Gehen Sie in das Verzeichnis, in welchem das Programm gespeichert ist, indem sie `cd pfad/zum/verzeichnis`eingeben\n",
+    "4. Geben Sie im Termial`python programm.py` ein.\n",
+    "\n",
+    "Falls Sie Windows verwenden, brauchen Sie beim ersten Aufruf etwas länger und müssen zusätzliche Schritte vornehmen, bei weiterer Verwendung springen Sie direkt zu Punkt 2 der Anleitung:\n",
+    "1. Fügen Sie Python zur PATH- Umgebung hinzu:  \n",
+    "    1.1. Finden Sie heraus wo Anaconda und Python gespeichert sind. (Dafür geben sie im Anaconda Prompt `where anaconda`und `where python` ein)  \n",
+    "    1.2. Öffnen Sie den Explorer und öffnen Sie das Rechtsklick-Menü von `Dieser PC`  \n",
+    "    1.3. Wählen Sie Eigenschaften  \n",
+    "    1.4. Wählen Sie Erweiterte Systemeinstellungen  \n",
+    "    1.5. Wählen Sie Umgebungsvariablen  \n",
+    "    1.6. Klicken Sie `Path`im unteren fenster an und dann auf `bearbeiten`  \n",
+    "    1.7. Klicken Sie auf `neu`und fügen Sie den Pfad für `Anaconda` hinzu, aber lassen Sie `anaconda.exe` weg  \n",
+    "    1.8. Wiederholen Sie dasselbe analog für den `Python` Pfad, dabei lassen Sie `python.exe` weg.  \n",
+    "    1.9. Klicken Sie 2 mal okay und schließen Sie die Systemsteuerung  \n",
+    "    1.10. Öffnen Sie die Kommandozeile (`cmd` in der Suchleiste eingeben und `enter` drücken) und geben sie `python` oder `python.exe` ein. Wenn Sie Erfolg hatten, öffnet sich Python und Sie könnten in der Kommandozeile programmieren.  \n",
+    "    1.11. Verlassen Sie `python` indem sie `exit()` eingeben.  \n",
+    "2. Speichern Sie das Programm, das sie aufrufen möchten als Python Programm (.py)\n",
+    "3. Geben Sie in der Kommandozeile `python.exe` und den Pfad zu Ihrem Programm ein (also `C:\\Users\\IhrName\\Documents\\nested\\programm.py`)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "### 4.1 Das `turtle`-Modul\n",
     "\n",
     "Führen Sie den folgenden Code aus, um zu testen, ob das `turtle`-Modul installiert ist:"
@@ -68,9 +105,10 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Es sollte sich ein Fenster öffnen, in dem ein kleiner Pfeil zu sehen ist - dieser repräsentiert die Schildkröte (\"turtle\"). Schließen Sie das Fenster.\n",
+    "Es sollte sich ein Fenster öffnen, in dem ein kleiner Pfeil zu sehen ist -- dieser repräsentiert die Schildkröte (\"turtle\"). Schließen Sie das Fenster.\n",
     "\n",
-    "*(Hinweis: In Jupyter gibt es manchmal Probleme mit dem `turtle`-Modul. Dann hilft es, das Turtle-Fenster zu schließen und den Code nochmal auszuführen oder im Kernel-Menü den Punkt \"Restart & Clear Output\" aufzurufen. Wenn es gar nicht klappt, dann nutzen Sie für die Turtle-Programmierung bitte nicht Jupyter-Notebooks, sondern Python-Dateien und führen diese direkt mit Python aus.)*\n",
+    "*(Hinweis: In Jupyter gibt es manchmal Probleme mit dem `turtle`-Modul. Dann hilft es, das Turtle-Fenster zu schließen und den Code nochmal auszuführen oder im Kernel-Menü den Punkt \"Restart & Clear Output\" aufzurufen. Wenn es gar nicht klappt, dann nutzen Sie für die Turtle-Programmierung bitte nicht Jupyter-Notebooks, sondern Python-Dateien und führen diese direkt mit Python aus.   \n",
+    "Manchmal vergisst Jupyter Notebooks auch, dass bereits eine Schildkröte existiert, in diesem Fall initialisieren Sie diese bitte einfach am Anfang des gewünschten Code-Blocks)*\n",
     "\n",
     "Probieren Sie nun folgendes (am besten in einem eigenen Jupyter-Notebook, einer eigenen Python-Datei, oder im folgenden Block, den Sie dann schrittweise ergänzen):"
    ]
@@ -89,6 +127,13 @@
     "turtle.bye()"
    ]
   },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
   {
    "cell_type": "markdown",
    "metadata": {},
@@ -101,9 +146,9 @@
     "\n",
     "Das bedeutet, dass `bob` auf ein Objekt vom Typ `Turtle` verweist, wie es im `turtle`-Modul definiert wurde.\n",
     "\n",
-    "Der Aufruf von `mainloop` weist das Fenster an, auf Nutzeraktivität zu warten. In diesem Fall kann man als Nutzerin allerdings kaum mehr tun, als das Fenster zu schließen.\n",
+    "Der Aufruf von `mainloop` weist das Fenster an, auf Nutzeraktivität zu warten. In diesem Fall kann man als NutzerIn allerdings kaum mehr tun, als das Fenster zu schließen.\n",
     "\n",
-    "Sobald wir eine Schildkröte erzeugt haben, können wir eine **Methode** aufrufen, um die Schildkröte über das Fenster zu bewegen. Eine Methode ist wie eine Funktion, aber die Syntax ist etwas anders. Z.B. können wir die Schildkröte mit dem Aufruf von \n",
+    "Sobald wir eine Schildkröte erzeugt haben, können wir eine **Methode** aufrufen, um die Schildkröte im Fenster zu bewegen. Eine Methode ist einer Funktion ähnlich, aber die Syntax ist etwas anders. Zum Beispiel können wir die Schildkröte mit dem Aufruf von \n",
     "\n",
     "```python\n",
     "bob.fd(100)\n",
@@ -115,7 +160,7 @@
     "\n",
     "Andere Methoden, die wir auf einer Schildkröte aufrufen können sind `bk` für eine Rückwärtsbewegung (**b**ac**k**ward), `lt` für eine Linksdrehung (**l**eft **t**urn) und `rt` für eine Rechtsdrehung (**r**ight **t**urn). Das Argument für `lt` und `rt` ist ein Winkel in Grad.\n",
     "\n",
-    "Jede Schildkröte hat außerdem einen Stift, der entweder oben oder unten ist. Wenn der Stift unten ist, hinterlässt die Schildkröte eine Spur, wenn sie sich bewegt. Die Methoden `pu` und `pd` stehen für \"Stift hoch\" (**p**en **u**p) und \"Stift herunter\" (**p**en **d**own).\n",
+    "Jede Schildkröte hat außerdem einen \"Stift\", der entweder \"oben\" oder \"unten\" ist. Wenn der Stift unten ist, berührt der Stift sozusagen das Papier und die Schildkröte hinterlässt eine Spur wenn sie sich bewegt. Die Methoden `pu` und `pd` stehen für \"Stift hoch\" (**p**en **u**p) und \"Stift herunter\" (**p**en **d**own).\n",
     "\n",
     "Fügen Sie die folgenden Zeilen zu Ihrem Programm hinzu, um einen rechten Winkel zu zeichnen (nachdem Sie `bob` erzeugt haben und bevor Sie `mainloop` aufrufen):\n",
     "\n",
@@ -166,7 +211,8 @@
    "outputs": [],
    "source": [
     "for i in range(4):\n",
-    "    print('Hello!')"
+    "    print('Hello!')\n",
+    "    "
    ]
   },
   {
@@ -188,19 +234,27 @@
     "\n",
     "(Quelle: Jason Eppink, Flickr)\n",
     "\n",
-    "Folgende `for`-Schleife zeichnet ein Quadrat:\n",
+    "Folgende `for`-Schleife zeichnet ein Quadrat:\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "bob=turtle.Turtle()\n",
     "\n",
-    "```python\n",
     "for i in range(4):\n",
     "    bob.fd(100)\n",
-    "    bob.lt(90)\n",
-    "```\n",
-    "\n",
-    "Die Syntax für die `for`-Schleife ist ähnlich einer Funktionsdefinition: Es gibt einen (Schleifen-)Kopf, der mit einem Doppelpunkt endet und einen eingerückten (Schleifen-)Rumpf. Im Rumpf können beliebig viele Anweisungen stehen.\n",
-    "\n",
-    "Man nennt dies eine **Schleife**, denn der Rumpf wird abgearbeitet und dann beginnt der Kontrollfluss wieder von vorn. In unserem Beispiel wird der Rumpf viermal durchlaufen.\n",
-    "\n",
-    "Dieser Code ist etwas anders als der vorherige Code zum Zeichnen eines Quadrats, denn nachdem die letzte Seite des Quadrats gezeichnet wurde wird noch eine weitere Drehung durchgeführt. Diese zusätzliche Drehung kostet etwas Zeit, aber der Code ist etwas einfacher, wenn in jedem Schleifendurchlauf immer die gleiche Folge von Anweisungen ausgeführt wird. Ein Nebeneffekt ist, dass die Schildkröte am Ende wieder in der Ausgangsposition ist mit Blickrichtung zur Ausgangsrichtung.\n"
+    "    bob.lt(90)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Dieser Code ist etwas anders als der vorherige Code zum Zeichnen eines Quadrats. Nachdem die letzte Seite des Quadrats gezeichnet wird, wird noch eine 90° Drehung durchgeführt. Diese zusätzliche Drehung kostet etwas Zeit, aber der Code ist einfacher, wenn in jedem Schleifendurchlauf die gleiche Folge von Anweisungen ausgeführt wird. Ein Nebeneffekt ist, dass die Schildkröte am Ende wieder in der Ausgangsposition mit Blick zur Ausgangsrichtung steht."
    ]
   },
   {
@@ -209,18 +263,7 @@
    "source": [
     "###  4.3 Ãœbungen\n",
     "\n",
-    "Es folgen einige Übungen zur \"Schildkrötenwelt\". Sie sollen Ihnen Spaß bereiten, aber die Übungen haben auch eine Bedeutung. Überlegen Sie, was das sein könnte, während Sie daran arbeiten.\n",
-    "\n",
-    "1. Schreiben Sie eine Funktion `square`, die einen Parameter namens `t` erwartet, welcher eine Schildkröte ist. Die Funktion soll die Schildkröte nutzen, um ein Quadrat zu zeichnen.\n",
-    "\n",
-    "2. Schreiben Sie einen Funktionsaufruf, der `bob` als Argument an `square` übergibt und rufen Sie ihr Programm wieder auf.\n",
-    "3. Ergänzen Sie die Funktion `square` um einen weiteren Parameter namens `length`. Ändern Sie den Rumpf der Funktion, so dass dass die Seitenlänge des gezeichneten Quadrats `length` entspricht. Passen Sie dann den Funktionsaufruf an, so dass ein weiteres Argument als Länge übergeben wird. Starten Sie ihr Programm noch einmal und testen Sie es mit verschiedenen Werten für die Länge.\n",
-    "4. Kopieren Sie die Definition der Funktion `square` und benennen Sie die Kopie in `polygon` um. Fügen Sie einen weiteren Parameter namens `n` hinzu und ändern Sie den Funktionsrumpf, so dass ein n-seitiges [reguläres Vieleck](https://de.wikipedia.org/wiki/Regelm%C3%A4%C3%9Figes_Polygon) (Polygon) gezeichnet wird. *Tipp: Die Außenwinkel eines n-seitigen Vielecks betragen 360/n Grad.* \n",
-    "5. Schreiben Sie eine Funktion `circle` die eine Schildkröte `t` und einen Radius `r` als Parameter erwartet und annähernd einen Kreis zeichnet, indem die Funktion `polygon` mit einer geeigneten Seitenlänge und Anzahl von Seiten aufruft. Testen Sie ihre Funktion mit verschiedenen Werten für `r`.\n",
-    "\n",
-    "   *Tipp: Finden Sie den Umfang des Kreises heraus und stellen Sie sicher, dass `length * n` gleich dem Umfang ist.*\n",
-    "   \n",
-    "6. Schreiben Sie eine verallgemeinerte Funktion `circle`, die Sie `arc` nennen, die ein weiteres Argument `angle` erwartet, welches angibt, welcher Teil eines Kreises gezeichnet werden soll. Die Funktion `arc` soll also einen Kreisbogen zeichnen. Der Wert von `angle` ist dabei in Grad, so dass für `angle=360` ein vollständiger Kreis gezeichnet werden sollte."
+    "In den folgenden Abschnitten folgen einige Übungen zur \"Schildkrötenwelt\". Sie sollten Ihnen Spaß bereiten, habe aber auch einen Sinn. Versuchen Sie diesen herauszufinden und gehen Sie Abschnittweise vor. \n"
    ]
   },
   {
@@ -229,6 +272,24 @@
    "source": [
     "### 4.4 Verkapselung\n",
     "\n",
+    " - **Aufgabe 1:** Schreiben Sie eine Funktion `square`, die einen Parameter namens `t` erwartet, welcher eine Schildkröte ist. Die Funktion soll die Schildkröte nutzen, um ein Quadrat zu zeichnen.\n",
+    " - **Aufgabe 2:** Schreiben Sie einen Funktionsaufruf, der `bob` als Argument an `square` übergibt und rufen Sie ihr Programm auf."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)\n",
     "\n",
     "In der ersten Aufgabe sollten Sie den Code zum Zeichnen eines Quadrates in eine Funktion packen und dann in Aufgabe 2 die Funktion aufrufen, indem Sie eine Schildkröte als Argument an die Funktion übergeben. So könnte eine mögliche Lösung aussehen:"
    ]
@@ -251,7 +312,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Die beiden innersten Anweisungen (`t.fd` und `t.lt`) sind doppelt eingerückt, weil sie innerhalb der `for`-Schleife sind, die innerhalb der Funtionsdefinition steht. Die übernächste Zeile (`square(bob)`) ist wieder bündig mit dem linken Rand ausgerichtet, also sowohl außerhalb der `for`-Schleife als auch außerhalb der Funktionsdefinition.\n",
+    "Die beiden innersten Anweisungen (`t.fd` und `t.lt`) sind doppelt eingerückt, weil sie innerhalb der `for`-Schleife sind, die wiederrum innerhalb der Funktionsdefinition steht. Die übernächste Zeile (`square(bob)`) ist wieder bündig mit dem linken Rand ausgerichtet, also sowohl außerhalb der `for`-Schleife, als auch außerhalb der Funktionsdefinition.\n",
     "\n",
     "Innerhalb der Funktion verweist `t` auf die gleiche Schildkröte `bob`, so dass `t.lt(90)` die gleiche Auswirkung hat wie `bob.lt(90)`. Hätten wir dann in der Funktion nicht direkt `bob` aufrufen können oder den Parameter stattdessen `bob` nennen können? Prinzipiell schon, aber die Idee ist, dass `t` irgendeine Schildkröte sein kann, nicht nur `bob`, so dass wir beispielsweise eine zweite Schildkröte erzeugen und sie als Argument an `square` übergeben können:"
    ]
@@ -270,9 +331,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Ein Stück Quellcode in eine Funktion zu \"packen\" nennt man \"Verkapselung\" (Englisch: *encapsulation*). Ein Vorteil der Verkapselung ist, dass für ein Stück Code ein Name vergeben wird, der wie eine Art Dokumentation wirkt, also sagt, was der Code macht. Ein anderer Vorteil ist, dass wir den Code leicht wiederverwenden können, denn es ist deutlich praktischer, eine Funktion zweimal aufzurufen, statt den Quellcode im Funktionsrumpf zu kopieren.\n",
-    "\n",
-    "[zurück](#4.3-%C3%9Cbungen)"
+    "Ein Stück Quellcode in eine Funktion zu packen, nennt man \"Verkapselung\" (Englisch: *encapsulation*). Ein Vorteil der Verkapselung ist, dass für ein Stück Code ein Name vergeben wird, der wie eine Art Dokumentation wirkt, also sagt, was der Code macht. Ein anderer Vorteil ist, dass wir den Code leicht wiederverwenden können, denn es ist deutlich praktischer, eine Funktion zweimal aufzurufen, als den Quellcode im Funktionsrumpf zu kopieren."
    ]
   },
   {
@@ -281,7 +340,25 @@
    "source": [
     "### 4.5 Verallgemeinerung\n",
     "\n",
-    "Der nächste Schritt ist, einen Parameter `length` zu `square` hinzuzufügen. Hier ist eine Lösung:"
+    "- **Aufgabe 3:** Ergänzen Sie die Funktion `square` um einen weiteren Parameter namens `length`. Ändern Sie den Rumpf der Funktion so, dass dass die Seitenlänge des gezeichneten Quadrats `length` entspricht. Passen Sie dann den Funktionsaufruf an, sodass ein weiteres Argument als Länge übergeben wird. Starten Sie ihr Programm noch einmal und testen Sie es mit verschiedenen Werten für die Länge. *(Hinweis: Kopieren Sie die Funktion aus dem vorherigen Abschnitt oder arbeiten Sie in dem bereits geschriebenen Code)*"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Der nächste Schritt ist, einen Parameter `length` zu `square` hinzuzufügen. Hier ist eine Lösung:\n",
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)"
    ]
   },
   {
@@ -295,16 +372,34 @@
     "        t.fd(length)\n",
     "        t.lt(90)\n",
     "\n",
-    "square(bob, 100)"
+    "square(bob, 400)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Das Hinzufügen des Parameters stellt eine **Verallgemeinerung** dar; denn die Funktion wird dadurch allgemeiner: vorher hatte das gezeichnete Quadrat immer die gleiche Größe, jetzt kann es jede beliebige Größe haben.\n",
+    "\n",
+    "- **Aufgabe 4:** Kopieren Sie die Definition der Funktion `square` und benennen Sie die Kopie in `polygon` um. Fügen Sie einen weiteren Parameter namens `n` hinzu und ändern Sie den Funktionsrumpf so, dass ein n-seitiges [reguläres Vieleck](https://de.wikipedia.org/wiki/Regelm%C3%A4%C3%9Figes_Polygon) (Polygon) gezeichnet wird. *(Hinweis: Die Außenwinkel eines n-seitigen Vielecks betragen 360/n Grad.)*"
    ]
   },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Das Hinzufügen des Parameters stellt eine **Verallgemeinerung** dar, denn die Funktion wird dadurch allgemeiner: vorher hatte das gezeichnete Quadrat immer die gleiche Größe, jetzt kann es jede beliebige Größe haben.\n",
+    "Der nächste Schritt ist ebenfalls eine Verallgemeinerung. Anstatt eines Quadrates kann die Funktion `polygon` reguläre Vielecke mit beliebig vielen Seiten zeichnen. So könnte eine Lösung aussehen:\n",
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
     "\n",
-    "Der nächste Schritt ist ebenfalls eine Verallgemeinerung. Anstatt eines Quadrates kann die Funktion `polygon` reguläre Vielecke mit beliebig vielen Seiten zeichnen. So könnte eine Lösung aussehen:"
+    "(Quelle: Jason Eppink, Flickr)"
    ]
   },
   {
@@ -355,7 +450,27 @@
    "source": [
     "### 4.6 Schnittstellenentwurf\n",
     "\n",
-    "Der nächste Schritt ist, eine Funktion `circle` zu schreiben, die einen Radius `r` als Parameter erwartet. Hier eine einfache Lösung, die die Funktion `polygon` nutzt, um ein reguläres 50-seitiges Vieleck zu zeichnen:"
+    "- **Aufgabe 5:** Schreiben Sie eine Funktion `circle` die eine Schildkröte `t` und einen Radius `r` als Parameter erwartet und annähernd einen Kreis zeichnet, indem sie die Funktion `polygon` mit einer geeigneten Seitenlänge und Anzahl von Seiten aufruft. Testen Sie ihre Funktion mit verschiedenen Werten für `r`.\n",
+    "\n",
+    "   *(Hinweis: Finden Sie den Umfang des Kreises heraus und stellen Sie sicher, dass `length * n` gleich dem Umfang ist.)*"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Der nächste Schritt ist, eine Funktion `circle` zu schreiben, die einen Radius `r` als Parameter erwartet. Hier eine einfache Lösung, die die Funktion `polygon` nutzt, um ein reguläres 50-seitiges Vieleck zu zeichnen:\n",
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)"
    ]
   },
   {
@@ -379,7 +494,7 @@
    "source": [
     "Die erste Zeile berechnet den Umfang eines Kreises mit dem Radius `r` mit Hilfe der Formel 2 π r. Da wir `math.pi` nutzen wollen, müssen wir zunächst `math` importieren. Die Konvention ist, dass `import`-Anweisungen stets am Anfang eines Python-Programms stehen.\n",
     "\n",
-    "Weil `n` die Anzahl der Liniensegmente in unserer Näherung eines Kreises ist, so ist `length` die Länge jedes einzelnen Segmentes. Daher zeichnet `polygon` ein reguläre 50-seitiges Vieleck als Näherun eines Kreises mit Radius `r`.\n",
+    "Weil `n` die Anzahl der Liniensegmente in unserer Näherung eines Kreises ist, ist `length` die Länge jedes einzelnen Segmentes. Daher zeichnet `polygon` ein reguläre 50-seitiges Vieleck als Näherun eines Kreises mit Radius `r`.\n",
     "\n",
     "Eine Beschränkung dieser Lösung ist, dass `n` eine Konstante ist. Daher sind für sehr große Kreise die Liniensegmente zu lang und für kleine Kreise verschwenden wir Zeit mit dem Zeichnen sehr kleiner Segmente. Eine Lösung wäre, die Funktion zu verallgemeinern und `n` als Parameter hinzuzufügen. Dies gäbe dem Nutzer (wer auch immer `circle` aufruft) mehr Kontrolle, aber die Schnittstelle wäre weniger aufgeräumt.\n",
     "\n",
@@ -387,7 +502,7 @@
     "\n",
     "In unserem Beispiel gehört `r` zur Schnittstelle, da es den Kreis beschreibt, der gezeichnet werden soll. Dagegen ist `n` weniger passend, denn es gehört zu den Details, wie der Kreis gezeichnet wird. \n",
     "\n",
-    "Anstatt die Schnittstelle zu \"verunreinigen\" ist es besser, einen passenden Wert von `n` in Abhängigkeit vom Umfang des Kreises zu wählen:"
+    "Anstatt die Schnittstelle zu \"verunreinigen\" ist es besser, einen passenden Wert für `n` in Abhängigkeit vom Umfang des Kreises zu wählen:"
    ]
   },
   {
@@ -407,15 +522,34 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Jetzt ist die Anzahl der Liniensegmente eine ganze Zahl, nahe bei Umfang/3, so dass die Länge jedes Segments ungefähr 3 beträgt. Das ist klein genug, damit der Kreis gut aussieht, aber auch groß genug, um eine effiziente Zeichnung zu ermöglichen und passt für jede Größe von Kreis. \n",
+    "Jetzt ist die Anzahl der Liniensegmente eine ganze Zahl, die nah bei Umfang/3 liegt, sodass die Länge jedes Segments ungefähr 3 beträgt. Das ist klein genug, damit der Kreis gut aussieht, aber auch groß genug, um eine effiziente Zeichnung zu ermöglichen und passt daher für jede Größe von Kreis. \n",
     "\n",
-    "Wir fügen 3 hinzu, damit das Vieleck mindestens drei Seiten hat.\n",
+    "Wir  addieren 3, damit das Vieleck mindestens drei Seiten hat.\n",
     "\n",
     "### 4.7 Refactoring\n",
     "\n",
+    "- **Aufgabe 6:** Schreiben Sie eine verallgemeinerte Funktion `circle`, die Sie `arc` nennen. Diese soll ein weiteres Argument `angle` erwartet, welches angibt, welcher Anteil des Kreises gezeichnet werden soll. Die Funktion `arc` soll also einen Kreisbogen zeichnen. Der Wert von `angle` ist dabei in Grad, so dass für `angle=360` ein vollständiger Kreis gezeichnet werden sollte.\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "Als wir `circle` geschrieben haben, konnten wir `polygon` wiederverwenden, denn ein regelmäßiges Vieleck mit vielen Seiten ist eine gute Näherung für einen Kreis. Aber mit der Funktion `arc` klappt das nicht so einfach - wir können kein Vieleck und keinen Kreis nutzen, um einen Kreisbogen zu zeichnen.\n",
     "\n",
-    "Eine Alternative ist, mit einer Kopie von `polygon` zu beginnen und diese zu `arc` zu verändern. Das Ergebnis könnte so aussehen:\n"
+    "Eine Alternative ist, mit einer Kopie von `polygon` zu beginnen und diese zu `arc` zu verändern. Das Ergebnis könnte so aussehen:\n",
+    "\n",
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)"
    ]
   },
   {
@@ -458,7 +592,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Jetzt können wir die Funktionen `polygon` und `arc` umschreiben, so dass sie die Funktion `polyline` nutzen:"
+    "Jetzt können wir die Funktionen `polygon` und `arc` umschreiben, sodass sie die Funktion `polyline` nutzen:"
    ]
   },
   {
@@ -483,7 +617,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Und schließlich können wir die Funktion `circle` umschreiben, so dass sie die Funktion `arc` nutzt:"
+    "Und schließlich können wir die Funktion `circle` umschreiben, sodass sie die Funktion `arc` nutzt:"
    ]
   },
   {
@@ -500,7 +634,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Dieser Prozess der Umstrukturierung eines Programms und der Verbesserung von Schnittstellen, um Code wiederverwenden zu können, nennt sich **Refactoring**. In unserem Fall haben wir festgestellt, dass `arc` und `polygon` ähnlichen Code enthalten haben, daher haben wir diesen Code umgestaltet und in die Funktion `polyline` \"ausfaktorisiert\" (es gibt leider keine gute Deutsche Übersetzung für dieses Vorgehen).\n",
+    "Dieser Prozess der Umstrukturierung eines Programms und der Verbesserung von Schnittstellen nennt sich **Refactoring** und hilft Code wiederverwenden zu können. In unserem Fall haben wir festgestellt, dass `arc` und `polygon` ähnlichen Code enthalten haben, daher haben wir diesen Code umgestaltet und in die Funktion `polyline` \"ausfaktorisiert\" also quasi ausgeklammert.\n",
     "\n",
     "Hätten wir vorausschauend geplant, hätten wir vielleicht `polyline` zuerst geschrieben und diese Umstrukturierung vermieden. Oft wissen wir aber am Anfang eines Projektes noch nicht genug, um schon alle Schnittstellen entwerfen zu können. Sobald wir anfangen zu programmieren, verstehen wir das Problem besser. Manchmal ist Refactoring ein Anzeichen dafür, dass wir etwas gelernt haben.\n"
    ]
@@ -517,9 +651,10 @@
     "2. Sobald das Programm funktioniert, identifizieren wir ein schlüssiges und zusammengehöriges Stück Code, verkapseln es in einer Funktion und geben ihm einen Namen.\n",
     "3. Wir verallgemeinern die Funktion durch Hinzufügen geeigneter Parameter.\n",
     "4. Wir wiederholen die Schritte 1 bis 3 bis wir eine Menge funktionierender Funktionen haben. Dabei kopieren wir Code und fügen ihn an der richtigen Stelle ein, um nochmaliges Eintippen zu vermeiden (und das damit ggf. verbundene Debugging).\n",
-    "5. Wir suchen nach Möglichkeiten, das Programm durch Refactoring zu verbessern. Wenn wir beispielsweise ähnlichen Code an verschiedenen Stellen haben, können wir überlegen, ob wir ihn nicht besser in eine geeignete allgemeine Funktion \"faktorisieren\". \n",
+    "5. Wir suchen nach Möglichkeiten, das Programm durch Refactoring zu verbessern. Wenn wir beispielsweise ähnlichen Code an verschiedenen Stellen haben, können wir überlegen, ob wir ihn nicht besser in eine geeignete allgemeine Funktion ausklammern. \n",
+    "\n",
     "\n",
-    "Dieser Prozess hat einige Nachteile (wir schauen uns Alternativen später an), aber er ist praktisch, wenn wir nicht vorab wissen, wie wir das Programm in Funktionen aufteilen könnten. Dieser Ansatz ermöglicht uns den Entwurf des Programms während wir es schreiben.\n"
+    "Dieser Prozess hat einige Nachteile (wir schauen uns Alternativen später an), aber er ist praktisch, wenn wir vorab nicht wissen, wie wir das Programm in Funktionen aufteilen könnten. Dieser Ansatz ermöglicht uns den Entwurf des Programms während wir es schreiben.\n"
    ]
   },
   {
@@ -528,7 +663,7 @@
    "source": [
     "### 4.9 Docstring\n",
     "\n",
-    "Ein **Docstring** ist eine Zeichenkette am Anfang einer Funktion die die Schnittstelle der Funktion erklärt (\"doc\" ist kurz für \"documentation\", also Dokumentation). Hier ist ein Beispiel:"
+    "Ein **Docstring** ist eine Zeichenkette am Anfang einer Funktion, die die Schnittstelle der Funktion erklärt (\"doc\" ist kurz für \"documentation\", also Dokumentation). Hier ist ein Beispiel:"
    ]
   },
   {
@@ -571,7 +706,7 @@
     "- `length` muss eine positive Zahl sein,\n",
     "- `angle` muss eine Zahl sein, die einen Winkel in Grad darstellt.\n",
     "\n",
-    "Diese Anforderungen nennen wir auch **Vorbedingungen**, denn es wird vorausgesetzt, dass sie erfüllt sind, bevor die Funktion ausgeführt wird. Umgekehrt heißen Bedingungen am Ende einer Funktion **Nachbedingungen**. Nachbedingungen schließen die beabsichtigte Wirkung der Funktion (wie z.B. ein Linienstück zeichnen) und etwaige Seiteneffekte (wie z.B. die Schildkröte zu bewegen oder andere Änderungen vorzunehmen) ein.  \n",
+    "Diese Anforderungen nennen wir auch **Vorbedingungen**, denn es wird vorausgesetzt, dass sie erfüllt sind, bevor die Funktion ausgeführt wird. Umgekehrt heißen Bedingungen am Ende einer Funktion **Nachbedingungen**. Nachbedingungen schließen die beabsichtigte Wirkung der Funktion (wie z.B. ein Linienstück zeichnen) und etwaige Nebeneffekte (wie z.B. die Schildkröte zu bewegen oder andere Änderungen vorzunehmen) ein.  \n",
     "\n",
     "Die Erfüllung der Vorbedingungen ist die Aufgabe der Aufrufenden. Wenn die Aufrufenden eine (ordentlich dokumentierte!) Vorbedingung verletzen und die Funktion arbeitet nicht richtig, dann liegt der Fehler bei den Aufrufenden, nicht bei der Funktion.\n",
     "\n",
@@ -586,13 +721,13 @@
     "\n",
     "Legen wir uns eine Liste mit den wichtigsten Begriffen an, die wir im Kapitel 4 gelernt haben:\n",
     "\n",
-    "- Methode: Eine Funktion, die zu einem Objekt gehört und mit Hilfe der Punktnotation aufgerufen wird.\n",
-    "- Schleife: \n",
+    "- Methode:\n",
+    "- Schleife: Eine Schleife ist eine Folge von Anweisungen, die mehrfach hintereinander ausgeführt werden.\n",
     "- Verkapselung: \n",
     "- Verallgemeinerung:\n",
     "- Schlüsselwortargument:\n",
     "- Schnittstelle:\n",
-    "- Refactoring: Der Prozess, ein funktionierendes Programm zu verändern, um die Schnittstellen der Funktionen und andere Aspekte des Codes zu verbessern.\n",
+    "- Refactoring: \n",
     "- Entwicklungsplan:\n",
     "- Docstring:\n",
     "- Vorbedingung:\n",
@@ -609,7 +744,7 @@
     "\n",
     "#### Aufgabe 1\n",
     "\n",
-    "Laden Sie den Code für dieses Kapitel hier herunter: http://thinkpython2.com/code/polygon.py\n",
+    "Laden Sie den Code für dieses Kapitel [hier](http://thinkpython2.com/code/polygon.py) herunter.\n",
     "\n",
     "*Hinweis: Um Probleme mit Turtle+Jupyter zu vermeiden, stellen Sie sicher, dass am Ende Ihres Programmes stets die folgenden beiden Zeilen stehen:*"
    ]
@@ -628,40 +763,243 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "1. Zeichnen Sie (mit Stift und Papier) ein Stapeldiagramm (siehe [Kapitel 3](#3.9-Stapel-Diagramme)), welches den Zustand des Programms zeigt, während die Anweisung `circle(bob, radius)` ausgeführt wid. Sie können das manuell herausfinden, oder `print`-Anweisungen zum Code hinzufügen.\n",
-    "2. Die Version der Funktion `arc` in [Abschnitt 4.7](#4.7-Refactoring) ist nicht besonders präzise, denn die lineare Näherung eines Kreises ist immer ausserhalb des wahren Kreises. Daher steht die Schildkröte am Ende immer ein paar Pixel vom richtigen Ziel entfernt. Die Lösung im Python-Code zeigt eine Möglichkeit, die Auswirkung dieses Fehlers zu reduzieren. Lesen Sie sich den Code durch und schauen Sie, ob das für Sie einen Sinn ergibt. Vielleicht hilft es Ihnen weiter, ein Diagramm zu zeichnen.\n",
-    "\n",
+    "1. Zeichnen Sie (mit Stift und Papier) ein Stapeldiagramm (siehe [Kapitel 3](#3.9-Stapel-Diagramme)), welches den Zustand des Programms zeigt, während die Anweisung `circle(bob, radius)` ausgeführt wid. Sie können das manuell herausfinden, oder `print`-Anweisungen zum Code hinzufügen. (*Hinweis: Unter Umständen kann Ihnen [Python-Tutor](http://pythontutor.com/) dabei helfen*)\n",
+    "2. Die Version der Funktion `arc` in [Abschnitt 4.7](#4.7-Refactoring) ist nicht besonders präzise, denn die lineare Näherung eines Kreises ist immer ausserhalb des wahren Kreises. Daher steht die Schildkröte am Ende immer ein paar Pixel vom richtigen Ziel entfernt. Die Lösung im Python-Code zeigt eine Möglichkeit, die Auswirkung dieses Fehlers zu reduzieren. Lesen Sie sich den Code durch und schauen Sie, ob das für Sie einen Sinn ergibt. Vielleicht hilft es Ihnen weiter, ein Diagramm zu zeichnen."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
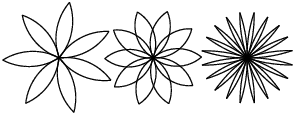
     "#### Aufgabe 2\n",
     "\n",
     "![Schildkröten-Blumen](http://greenteapress.com/thinkpython2/html/thinkpython2003.png)\n",
     "\n",
     "Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Blumen.\n",
     "\n",
-    "*(Die [Lösung](http://thinkpython2.com/code/flower.py) benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py).)*\n",
+    "*(Die Lösung benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py).)*\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "\n",
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)\n",
     "\n",
+    "1. Die Blumen bestehen aus 2 Teilen.... \n",
+    "2. Überlegen Sie erst, wie man ein einzelnes Blütenblatt zeichnen kann.\n",
+    "3. Welche Informationen müssen der Funktion in der Schnittstelle übergeben werden?\n",
+    "4. Die Funktion braucht eine Schildkröte, die Größe des Blütenblatts und Winkel in dem das Blütenblatt gezeichnet werden soll (also wie breit das Blütenblatt sein soll)\n",
+    "3. Jedes Blütenblatt besteht aus 2 Kreisbögen, also brauchen Sie arc (nutzen Sie ihre eigene Funktion oder kopieren Sie arc aus polygon.py)\n",
+    "4. Nach dem ersten Kreisbogen muss die Schildkröte sich soweit drehen, dass sie mit dem nächsten Kreisbogen eine volle 180° Drehung vollzogen hat\n",
+    "5. Wie können sie die Blütenblätter dann miteinander zu einer blume verbinden?\n",
+    "8. Was muss der Funktion Blume in der Schnittstelle an Argumenten übergeben werden? \n",
+    "9. Sie brauchen alle Argumente, die in der Funktion an Blatt übergeben werden und natürlich auch die Anzahl n an Blütenblättern, aus denen die Blume bestehen soll.\n",
+    "6. In Blume muss Blatt n mal aufgerufen werden \n",
+    "6. Um die Blütenblätter gleichmäßig um den Mittelpunkt der Blume zu verteilen, muss der Winkel zwischen den Blättern so berechnet werden, dass nach Vollenden der Blume eine 360° Wendung vollzogen wurde.\n",
+    "7. Dafür muss der Winkel zwischen den Blättern 360/n betragen\n",
+    "\n",
+    "Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/flower.py)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "import math\n",
+    "import turtle\n",
+    "bob=turtle.Turtle()\n",
+    "\n",
+    "# Damit diese Lösung funktioniert müssen def arc und def polyline bekannt sein.\n",
+    "\n",
+    "def blatt(t, r, angle):\n",
+    "    for i in range (2):\n",
+    "        arc(t,r, angle)\n",
+    "        t.lt(180.0-angle)\n",
+    "    \n",
+    "    \n",
+    "def blume(t,r,angle,n):\n",
+    "    for i in range (n):\n",
+    "        blatt (t,r,angle)\n",
+    "        t.lt(360/n)\n",
+    "\n",
+    "blume(bob,60.0,60.0,5)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "#### Aufgabe 3\n",
     "\n",
     "![Schildkröten-Kuchen](http://greenteapress.com/thinkpython2/html/thinkpython2004.png)\n",
     "\n",
     "Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Figuren.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "\n",
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "(Quelle: Jason Eppink, Flickr)\n",
+    "\n",
+    "1. Wir gehen analog zu Blume vor, und zeichnen die einzelnen \"Kuchenstücke\" bevor wir sie zu dem \"Kuchen\" zusammensetzen.\n",
+    "2. Wir müssen die obere Seitenlänge berechnen um sie zeichnen zu können. Sinus verwendet Bogenmaß, das heißt um die \"richtige\" Seitenlänge zu erhalten müssen wir den Winkel umrechnen. *Hinweiß: Dafür wird mit $\\pi/180$ multipliziert*\n",
+    "3. Die vollständige Formel ist $2*r*sin(angle*\\pi/180)$ \n",
+    "4. Über die 3 Seiten verteilt, muss sich die Schildkröte soweit drehen, dass sie wieder am Ausgangspunkt ankommen. \n",
+    "5. Sie muss zweimal die Strecke r laufen und dazwischen einmal die Strecke, die wir berechnet haben.\n",
+    "6. Dazwischen muss sich die Schildkröte immer drehen. Verwenden Sie dafür angle und Vielfältige von 90 und probieren Sie verschiedene Varienten aus, bis es funktioniert.\n",
+    "7. Damit kuchen später funktioniert, muss die Schildkröte wieder ihre Ausgangsposition Annehmen. Dafür fügen Sie noch je eine Drehung am Anfang und am Ende ein.\n",
+    "8. Für kuchen können Sie blume wiederverwenden, müssen allerdings einige Veränderungen vornehmen. Damit keine Lücken entstehen, muss die Funktion angle berechnen, statt diesen Wert übergehen zu bekommen. Dann muss auch der Winkel für Stück angepasst werden.\n",
+    "9. Um die Stücke zu verbinden wird in der for Schleife eine Drehung von 360/n vorgenommen. Die Drehung in Stück muss dann halb so groß sein. \n",
+    "\n",
+    "*(Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/pie.py))*"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "import math\n",
+    "import turtle\n",
+    "\n",
+    "def stück (t,r, angle):\n",
+    "    c=2*r*(math.sin(angle*math.pi/180))\n",
+    "    t.rt(angle)\n",
+    "    t.fd(r)\n",
+    "    t.lt(90+angle)\n",
+    "    t.fd(c)\n",
+    "    t.lt(90+angle)\n",
+    "    t.fd(r)\n",
+    "    t.lt(180-angle)\n",
+    "\n",
+    "\n",
     "\n",
-    "*([Lösung](http://thinkpython2.com/code/pie.py))*\n",
     "\n",
+    "def kuchen (t, n, r):\n",
+    "    angle=360/n\n",
+    "    for i in range (n):\n",
+    "        stück(t,r,angle/2)\n",
+    "        t.lt(angle)\n",
+    "    turtle.mainloop()\n",
+    "    turtle.bye()\n",
+    "        \n",
+    "        \n",
+    "        \n",
+    "   \n",
+    "    \n",
+    "    \n",
+    "bob=turtle.Turtle()  \n",
+    "kuchen(bob,4,40,40)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "#### Aufgabe 4\n",
     "\n",
-    "*(Hinweis: Dies ist eher eine Fleiß- und Zusatzaufgabe.)*\n",
     "\n",
-    "Die Buchstaben des Alphabets sind aus ein paar grundlegenden Elementen zusammengesetzt, wie z.B. vertikalen und horizontalen Linien und einigen Kurven. Entwerfen Sie ein Alphabet, welches mit einer kleinen Anzahl einfacher Elemente gezeichnet werden kann und schreiben Sie dann Funktionen zum Zeichnen der Buchstaben. \n",
+    "Lesen Sie etwas zu Spiralen auf [Wikipedia](https://de.wikipedia.org/wiki/Spirale). Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": []
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
+    "\n",
+    "1. Sie müssen sich entscheiden, welche Argumente Sie in der Schnittstelle übergeben wollen und welche Sie der Funktion übergeben wollen. (Hier habe ich mich entschieden, Nutzern verschiedene funktionierende Schleifen zur Auswahl zu geben)\n",
+    "2. In einem minimalistischen Schnittstellen Entwurf muss noch mindestens die Schildkröte an die Funktion übergeben werden.\n",
+    "3. Die Formel für die Berechnung von Spiralen ist $r = a + b\\theta$ , a können Sie auf 0.1 und b auf 0.0002 als Ausgangswerte festlegen. \n",
+    "4. Andere Parameterm die Sie entweder in der Schnittstelle oder in der Funktion festlegen müssen sind der Winkel theta, die Anzahl an Spiralensegmenten und die Länge der einzelnen Segmente. \n",
+    "5. Analog zum Kreisbogen wird auch die Spirale durch kurze gerade Segmente und Drehungen gezeichnet. Da das Zeichnen von Segmenten n-mal wiederholt wird, benötigen Sie eine for-Schleife.\n",
+    "6. In der Schleife muss für jedes Segment neu berechnet werden wie weit die Schildkröte sich drehen muss, da der Winkel nicht konstant bleibt. Dafür verwendet die Lösung: dtheta = 1 / (a + b * theta)\n",
+    "7. Da diese Formel theta als den Winkel des vorherigen Abschnitts verwendet, muss theta ebenfalls in jedem Schleifendurchlauf überschrieben werden - also addieren Sie dtheta auf theta auf. \n",
+    " \n",
     "\n",
-    "Sie sollten eine Funktion für jeden Buchstaben schreiben, die Sie `draw_a`, `draw_b`, etc. nennen und diese Funktionen in eine Datei namens `letters.py` packen. Sie können [hier](http://thinkpython2.com/code/typewriter.py) eine \"Schildkrötenschreibmaschine\" herunterladen und damit ihren Code testen.\n",
     "\n",
-    "Sie finden eine Lösung für diese Aufgabe hier: http://thinkpython2.com/code/letters.py; Diese benötigt auch http://thinkpython2.com/code/polygon.py.\n",
+    "Eine [Lösung](http://thinkpython2.com/code/spiral.py)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "def spirale(t,n):\n",
+    "    '''In dieser Spirale bestimmt der Nutzer, wie viele Segmente gezeichnet werden, die Windung der Spirale ist\n",
+    "    in der Funktion festgelegt.\n",
+    "    '''\n",
+    "    length=3 \n",
+    "    a=0.1\n",
+    "    b=0.0002\n",
+    "    theta=0.0\n",
+    "    for i in range (n):\n",
+    "        t.fd(length)\n",
+    "        dtheta = 1 / (a + b * theta)\n",
+    "        t.lt(dtheta)\n",
+    "        theta = theta + dtheta\n",
+    "\n",
+    "import turtle\n",
+    "bob=turtle.Turtle()        \n",
+    "spirale(bob,1000)\n",
+    "turtle.mainloop()\n",
+    "turtle.bye()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "\n",
     "#### Aufgabe 5\n",
     "\n",
-    "Lesen Sie etwas zu Spiralen auf Wikipedia: https://de.wikipedia.org/wiki/Spirale. Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n",
+    "*(Hinweis: Dies ist eher eine Fleiß- und Zusatzaufgabe.)*\n",
+    "\n",
+    "Die Buchstaben des Alphabets sind aus ein paar grundlegenden Elementen zusammengesetzt wie z.B. vertikalen und horizontalen Linien und einigen Kurven. Entwerfen Sie ein Alphabet, welches mit einer kleinen Anzahl einfacher Elemente gezeichnet werden kann und schreiben Sie dann Funktionen zum Zeichnen der Buchstaben. \n",
+    "\n",
+    "Sie sollten eine Funktion für jeden Buchstaben schreiben, die Sie `draw_a`, `draw_b`, etc. nennen und diese Funktionen in eine Datei namens `letters.py` packen. Sie können [hier](http://thinkpython2.com/code/typewriter.py) eine \"Schildkrötenschreibmaschine\" herunterladen und damit ihren Code testen.\n",
+    "\n",
+    "\n",
+    "Das könnte dann so aussehen:\n",
+    "![Schreibmaschine](https://box.hu-berlin.de/f/fec51b18a8af4535b445/?dl=1)\n",
     "\n",
-    "Eine Lösung finden Sie hier: http://thinkpython2.com/code/spiral.py. "
+    "Sie finden eine Lösung für diese Aufgabe [hier](http://thinkpython2.com/code/letters.py); Diese benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py)."
    ]
   },
   {