From ef2eb46985227d6d8ab30f2b523fd6a717e22aba Mon Sep 17 00:00:00 2001
From: schwabmi <michel.j.schwab@gmail.com>
Date: Mon, 7 Dec 2020 15:03:20 +0100
Subject: [PATCH] added MB 91431
---
notebooks/seminar04.ipynb | 638 ++++++++++++++++++++++++++++++++------
1 file changed, 550 insertions(+), 88 deletions(-)
diff --git a/notebooks/seminar04.ipynb b/notebooks/seminar04.ipynb
index a899336..dd34522 100644
--- a/notebooks/seminar04.ipynb
+++ b/notebooks/seminar04.ipynb
@@ -4,16 +4,30 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "# Seminar Problemorientierte Programmierung\n",
- "\n",
- "## 4: Fallstudie: Schnittstellenentwurf\n",
+ "# 4: Fallstudie: Schnittstellenentwurf\n",
"[Chapter 4: Case Study: interface design](http://greenteapress.com/thinkpython/html/thinkpython005.html)\n",
"\n",
"In diesem Kapitel lernen wir anhand einer Fallstudie, wie wir Funktionen entwerfen können, die gut zusammenarbeiten.\n",
"\n",
"Wir lernen außerdem das `turtle`-Modul kennen, mit dessen Hilfe wir Graphiken erzeugen können.\n",
"\n",
- "### Ihre Lernziele\n",
+ "\n",
+ "**Auch hier gilt wieder: Stellen Sie sicher, dass Sie die Konzepte der vorherigen Notebooks verstanden haben bevor Sie fortfahren.**"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "<h1>Inhaltsverzeichnis<span class=\"tocSkip\"></span></h1>\n",
+ "<div class=\"toc\"><ul class=\"toc-item\"><li><span><a href=\"#Ihre-Lernziele\" data-toc-modified-id=\"Ihre-Lernziele-1\"><span class=\"toc-item-num\">1 </span>Ihre Lernziele</a></span></li><li><span><a href=\"#Exkurs:-Was-mir-an-Python-gefällt\" data-toc-modified-id=\"Exkurs:-Was-mir-an-Python-gefällt-2\"><span class=\"toc-item-num\">2 </span>Exkurs: Was mir an Python gefällt</a></span></li><li><span><a href=\"#Python-für-das-turtle-Modul\" data-toc-modified-id=\"Python-für-das-turtle-Modul-3\"><span class=\"toc-item-num\">3 </span>Python für das <code>turtle</code>-Modul</a></span></li><li><span><a href=\"#Das-turtle-Modul\" data-toc-modified-id=\"Das-turtle-Modul-4\"><span class=\"toc-item-num\">4 </span>Das <code>turtle</code>-Modul</a></span></li><li><span><a href=\"#Einfache-Wiederholung\" data-toc-modified-id=\"Einfache-Wiederholung-5\"><span class=\"toc-item-num\">5 </span>Einfache Wiederholung</a></span></li><li><span><a href=\"#4-Übungen\" data-toc-modified-id=\"4-Übungen-6\"><span class=\"toc-item-num\">6 </span>4 Übungen</a></span><ul class=\"toc-item\"><li><span><a href=\"#Verkapselung\" data-toc-modified-id=\"Verkapselung-6.1\"><span class=\"toc-item-num\">6.1 </span>Verkapselung</a></span></li><li><span><a href=\"#Verallgemeinerung\" data-toc-modified-id=\"Verallgemeinerung-6.2\"><span class=\"toc-item-num\">6.2 </span>Verallgemeinerung</a></span></li><li><span><a href=\"#Schnittstellenentwurf\" data-toc-modified-id=\"Schnittstellenentwurf-6.3\"><span class=\"toc-item-num\">6.3 </span>Schnittstellenentwurf</a></span></li><li><span><a href=\"#Refactoring\" data-toc-modified-id=\"Refactoring-6.4\"><span class=\"toc-item-num\">6.4 </span>Refactoring</a></span></li></ul></li><li><span><a href=\"#Ein-Entwicklungsplan\" data-toc-modified-id=\"Ein-Entwicklungsplan-7\"><span class=\"toc-item-num\">7 </span>Ein Entwicklungsplan</a></span></li><li><span><a href=\"#Docstring\" data-toc-modified-id=\"Docstring-8\"><span class=\"toc-item-num\">8 </span>Docstring</a></span></li><li><span><a href=\"#Debugging\" data-toc-modified-id=\"Debugging-9\"><span class=\"toc-item-num\">9 </span>Debugging</a></span></li><li><span><a href=\"#Glossar\" data-toc-modified-id=\"Glossar-10\"><span class=\"toc-item-num\">10 </span>Glossar</a></span></li><li><span><a href=\"#Übung\" data-toc-modified-id=\"Übung-11\"><span class=\"toc-item-num\">11 </span>Übung</a></span><ul class=\"toc-item\"><li><span><a href=\"#Aufgabe-1\" data-toc-modified-id=\"Aufgabe-1-11.1\"><span class=\"toc-item-num\">11.1 </span>Aufgabe 1</a></span></li><li><span><a href=\"#Aufgabe-2\" data-toc-modified-id=\"Aufgabe-2-11.2\"><span class=\"toc-item-num\">11.2 </span>Aufgabe 2</a></span></li><li><span><a href=\"#Aufgabe-3\" data-toc-modified-id=\"Aufgabe-3-11.3\"><span class=\"toc-item-num\">11.3 </span>Aufgabe 3</a></span></li><li><span><a href=\"#Aufgabe-4\" data-toc-modified-id=\"Aufgabe-4-11.4\"><span class=\"toc-item-num\">11.4 </span>Aufgabe 4</a></span></li><li><span><a href=\"#Aufgabe-5\" data-toc-modified-id=\"Aufgabe-5-11.5\"><span class=\"toc-item-num\">11.5 </span>Aufgabe 5</a></span></li></ul></li></ul></div>"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## Ihre Lernziele\n",
"\n",
"Beschreiben Sie in 2-3 Stichpunkten kurz was Sie im Seminar heute lernen wollen. Klicken Sie dazu doppelt auf diesen Text und bearbeiten Sie dann den Text:\n",
"\n",
@@ -22,7 +36,7 @@
"- \n",
"\n",
"\n",
- "### Exkurs: Was mir an Python gefällt\n",
+ "## Exkurs: Was mir an Python gefällt\n",
"\n",
"Man kann schnell und einfach ein Programm aufschreiben und testen. Man muss es weder kompilieren, noch viel \"unnötige\" Syntax kennen:"
]
@@ -46,9 +60,12 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.0 Python für das `turtle`-Modul\n",
+ "## Python für das `turtle`-Modul\n",
+ "\n",
+ "\n",
+ "Da das `turtle`-Modul in Jupyter-Notebooks eventuell nicht so gut funktioniert, kann es von Vorteil sein, `turtle` über die Kommandozeile aufzurufen. Dies ist prinzipiell auf allen Betriebssystemen möglich, aber auf Linux und MacOS deutlich einfacher als auf Windows. Sie können das Programm in Jupyter Notebooks schreiben und unter \"Datei -> Herunterladen als -> Python (.py)\" herunterladen und dann über die Kommandozeile öffnen.\n",
+ "\n",
"\n",
- "Da das `turtle`-Modul in Jupyter-Notebooks eventuell nicht so gut funktioniert, kann es von Vorteil sein, `turtle` über die Kommandozeile aufzurufen. Dies ist prinzipell auf allen Betriebssystemen möglich, aber auf Linux und MacOS deutlich einfacher als auf Windows.\n",
"\n",
"Falls Sie Linux nutzen, sollte Python bereits installiert sein. Um das gewünschte Programm zu öffnen tun Sie folgendes: \n",
"1. Speichern Sie das Programm, das sie aufrufen möchten als Python-Programm mit der Dateiendung `.py`.\n",
@@ -58,10 +75,12 @@
"5. Alternativ können Sie auch direkt `python /pfad/zum/verzeichnis/programm.py` eingeben. \n",
"\n",
"Falls Sie MacOS verwenden, gehen Sie folgendermaßen vor:\n",
- "1. Speichern Sie das Programm, dass Sie aufrufen möchten als Python-Programm mit der Dateiendug `.py`.\n",
+ "1. Speichern Sie das Programm, dass Sie aufrufen möchten als Python-Programm mit der Dateiendung `.py`.\n",
"2. Öffnen Sie das Terminal\n",
"3. Gehen Sie in das Verzeichnis, in welchem das Programm gespeichert ist, indem sie `cd /pfad/zum/verzeichnis`eingeben\n",
- "4. Geben Sie im Termial `python programm.py` ein.\n",
+ "4. Geben Sie im Terminal `python programm.py` ein.\n",
+ "5. Alternativ können Sie auch direkt `python /pfad/zum/verzeichnis/programm.py` eingeben. \n",
+ "\n",
"\n",
"Falls Sie Windows verwenden, brauchen Sie beim ersten Aufruf etwas länger und müssen zusätzliche Schritte vornehmen, bei weiterer Verwendung springen Sie direkt zu Punkt 2 der Anleitung:\n",
"1. Fügen Sie Python zur PATH-Umgebung hinzu: \n",
@@ -73,7 +92,7 @@
" 1.6. Klicken Sie `Path` im unteren Fenster an und dann auf `bearbeiten` \n",
" 1.7. Klicken Sie auf `neu`und fügen Sie den Pfad für `Anaconda` hinzu, aber lassen Sie `anaconda.exe` weg \n",
" 1.8. Wiederholen Sie dasselbe analog für den `Python`-Pfad, dabei lassen Sie `python.exe` weg. \n",
- " 1.9. Klicken Sie zwei mal okay und schließen Sie die Systemsteuerung \n",
+ " 1.9. Klicken Sie zweimal okay und schließen Sie die Systemsteuerung \n",
" 1.10. Öffnen Sie die Kommandozeile (`cmd` in der Suchleiste eingeben und `enter` drücken) und geben sie `python` oder `python.exe` ein. Wenn Sie Erfolg hatten, öffnet sich Python und Sie können in der Kommandozeile programmieren. \n",
" 1.11. Verlassen Sie `python` indem sie `exit()` eingeben. \n",
"2. Speichern Sie das Programm, das sie aufrufen möchten als Python-Programm mit der Dateiendung `.py`.\n",
@@ -84,7 +103,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.1 Das `turtle`-Modul\n",
+ "## Das `turtle`-Modul\n",
"\n",
"Führen Sie den folgenden Code aus, um zu testen, ob das `turtle`-Modul installiert ist:"
]
@@ -107,24 +126,32 @@
"source": [
"Es sollte sich ein Fenster öffnen, in dem ein kleiner Pfeil zu sehen ist -- dieser repräsentiert die Schildkröte (\"turtle\"). Schließen Sie das Fenster. (Danach erscheint ggf. eine Fehlermeldung -- nicht erschrecken, diese ist im Allgemeinen harmlos.) \n",
"\n",
- "*(Hinweis: In Jupyter gibt es manchmal Probleme mit dem `turtle`-Modul. **Wichtig ist, dass Sie stets das Turtle-Fenster schließen.** Manchmal hilft es, den Code nochmal auszuführen oder im Kernel-Menü den Punkt \"Restart & Clear Output\" aufzurufen. Wenn es gar nicht klappt, dann nutzen Sie für die Turtle-Programmierung bitte nicht Jupyter-Notebooks, sondern Python-Dateien und führen diese direkt mit Python aus. \n",
- "Manchmal vergisst Jupyter Notebooks auch, dass bereits eine Schildkröte existiert, in diesem Fall initialisieren Sie diese bitte einfach am Anfang des gewünschten Code-Blocks)*\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-info\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "In Jupyter gibt es manchmal Probleme mit dem `turtle`-Modul. **Wichtig ist, dass Sie stets das Turtle-Fenster schließen.** Manchmal hilft es, den Code nochmal auszuführen oder im Kernel-Menü den Punkt \"Restart & Clear Output\" aufzurufen. Wenn es gar nicht klappt, dann nutzen Sie für die Turtle-Programmierung bitte nicht Jupyter-Notebooks, sondern Python-Dateien und führen diese direkt mit Python aus. \n",
+ "Manchmal vergisst Jupyter Notebooks auch, dass bereits eine Schildkröte existiert, in diesem Fall initialisieren Sie diese bitte einfach am Anfang des gewünschten Code-Blocks. \n",
+ " </div> \n",
+ "</details>\n",
"\n",
"Probieren Sie nun Folgendes (am besten in einem eigenen Jupyter-Notebook, einer eigenen Python-Datei oder im folgenden Block, den Sie dann schrittweise ergänzen):"
]
},
{
- "cell_type": "code",
- "execution_count": null,
+ "cell_type": "markdown",
"metadata": {},
- "outputs": [],
"source": [
+ "```python\n",
"import turtle\n",
"bob = turtle.Turtle()\n",
"print(bob)\n",
"bob.fd(100)\n",
"turtle.mainloop() \n",
- "turtle.bye()"
+ "turtle.bye()\n",
+ "```"
]
},
{
@@ -184,7 +211,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.2 Einfache Wiederholung\n",
+ "## Einfache Wiederholung\n",
"\n",
"Vielleicht haben Sie Folgendes geschrieben:\n",
"\n",
@@ -228,7 +255,22 @@
"Hello!\n",
"```\n",
"\n",
- "Das ist die einfachste Art und Weise, eine `for`-Schleife zu verwenden. Wir werden uns das später ausführlicher anschauen. Für jetzt sollte das reichen, damit Sie ihr Programm zum Zeichnen eines Quadrats vereinfachen können. Bitte fahren Sie erst fort, wenn Sie ihr Programm mit Hilfe der `for`-Schleife vereinfacht haben.\n",
+ "Das ist die einfachste Art und Weise, eine `for`-Schleife zu verwenden. Wir werden uns das später ausführlicher anschauen. Für jetzt sollte das reichen, damit Sie Ihr Programm zum Zeichnen eines Quadrats vereinfachen können. Bitte fahren Sie erst fort, wenn Sie ihr Programm mit Hilfe der `for`-Schleife vereinfacht haben.\n",
+ "\n",
+ "Es sollte sich ein Fenster öffnen, in dem ein kleiner Pfeil zu sehen ist -- dieser repräsentiert die Schildkröte (\"turtle\"). Schließen Sie das Fenster. (Danach erscheint ggf. eine Fehlermeldung -- nicht erschrecken, diese ist im Allgemeinen harmlos.) \n",
+ "\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Die `for`-Schleife besteht aus insgesamt 3 Zeilen. Dem Code, der sich immer wieder wiederholt (schauen Sie sich dazu an, was Sie im vorherigen Schritt geschrieben haben) und der Anweisung, die angibt, wie häufig sich der Code wiederholt. \n",
+ "\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "Probieren Sie nun Folgendes (am besten in einem eigenen Jupyter-Notebook, einer eigenen Python-Datei oder im folgenden Block, den Sie dann schrittweise ergänzen):\n",
"\n",
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
"\n",
@@ -266,7 +308,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.3 Ãœbungen\n",
+ "## 4 Ãœbungen\n",
"\n",
"In den folgenden Abschnitten folgen einige Übungen zur \"Schildkrötenwelt\". Sie sollten Ihnen Spaß bereiten, haben aber auch einen Sinn. Versuchen Sie diesen herauszufinden und gehen Sie abschnittweise vor. \n"
]
@@ -275,10 +317,50 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.4 Verkapselung\n",
+ "### Verkapselung\n",
"\n",
" - **Aufgabe 1:** Schreiben Sie eine Funktion `square`, die einen Parameter `t` erwartet, welcher eine Schildkröte ist. Die Funktion soll die Schildkröte nutzen, um ein Quadrat zu zeichnen.\n",
- " - **Aufgabe 2:** Schreiben Sie einen Funktionsaufruf, der `bob` als Argument an `square` übergibt und rufen Sie ihr Programm auf."
+ " \n",
+ " \n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Sie haben diese Funktion bereits geschrieben. Wie können Sie die Anweisungen verkapseln?\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Schreiben Sie den Kopf der Funktion, überlegen Sie wie Sie die Parameterschildkröte nennen wollen?\n",
+ "\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Stellen Sie sicher, dass die Schildkröte in der Funktion immer gleich heißt (genau wie das Argument, das im Funktionsaufruf übergeben wird), sodass alle Anweisungen ausgeführt werden \n",
+ "\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ " - **Aufgabe 2:** Schreiben Sie einen Funktionsaufruf, der `bob` als Argument an `square` übergibt und rufen Sie ihr Programm auf.\n",
+ " \n",
+ " \n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Initialisieren Sie die Schildkröte `bob`, da es sein kann, dass die Schildkröte nicht gefunden wird. Übergeben Sie `square` die Variable `bob`.\n",
+ "\n",
+ " </div> \n",
+ "</details>"
]
},
{
@@ -307,7 +389,7 @@
"source": [
"import turtle\n",
"\n",
- "bob=turtle.Turtle()\n",
+ "bob = turtle.Turtle()\n",
"\n",
"def square(t):\n",
" for i in range(4):\n",
@@ -335,13 +417,6 @@
"metadata": {},
"outputs": [],
"source": [
- "import turtle\n",
- "\n",
- "def square(t):\n",
- " for i in range(4):\n",
- " t.fd(100)\n",
- " t.lt(90)\n",
- "\n",
"alice = turtle.Turtle()\n",
"square(alice)\n",
"\n",
@@ -358,16 +433,26 @@
"\n",
"\n",
"\n",
- "([Code Quality](https://xkcd.com/1513/), Randall Munroe)"
+ "([Code Quality](https://xkcd.com/1513/), Randall Munroe) [Erklärung des Comics](https://www.explainxkcd.com/wiki/index.php/1513:_Code_Quality) falls Sie mehr lesen wollen."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.5 Verallgemeinerung\n",
+ "### Verallgemeinerung\n",
"\n",
- "- **Aufgabe 3:** Ergänzen Sie die Funktion `square` um einen weiteren Parameter namens `length`. Ändern Sie den Rumpf der Funktion so, dass die Seitenlänge des gezeichneten Quadrats `length` entspricht. Passen Sie dann den Funktionsaufruf an, sodass ein weiteres Argument als Länge übergeben wird. Starten Sie ihr Programm noch einmal und testen Sie es mit verschiedenen Werten für die Länge. *(Hinweis: Kopieren Sie die Funktion aus dem vorherigen Abschnitt oder arbeiten Sie in dem bereits geschriebenen Code)*"
+ "- **Aufgabe 3:** Ergänzen Sie die Funktion `square` um einen weiteren Parameter namens `length`. Ändern Sie den Rumpf der Funktion so, dass die Seitenlänge des gezeichneten Quadrats `length` entspricht. Passen Sie dann den Funktionsaufruf an, sodass ein weiteres Argument als Länge übergeben wird. Starten Sie ihr Programm noch einmal und testen Sie es mit verschiedenen Werten für die Länge. \n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-info\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Kopieren Sie die Funktion aus dem vorherigen Abschnitt oder arbeiten Sie in dem bereits geschriebenen Code. So können Sie vermeiden, dass Fehler entstehen, die im vorherigen Abschnitt noch nicht vorhanden waren.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n"
]
},
{
@@ -415,7 +500,50 @@
"source": [
"Das Hinzufügen des Parameters stellt eine **Verallgemeinerung** dar; denn die Funktion wird dadurch allgemeiner: vorher hatte das gezeichnete Quadrat immer die gleiche Größe, jetzt kann es jede beliebige Größe haben.\n",
"\n",
- "- **Aufgabe 4:** Kopieren Sie die Definition der Funktion `square` und benennen Sie die Kopie in `polygon` um. Fügen Sie einen weiteren Parameter namens `n` hinzu und ändern Sie den Funktionsrumpf so, dass ein n-seitiges [reguläres Vieleck](https://de.wikipedia.org/wiki/Regelm%C3%A4%C3%9Figes_Polygon) (Polygon) gezeichnet wird. *(Hinweis: Die Außenwinkel eines n-seitigen Vielecks betragen 360/n Grad.)*"
+ "- **Aufgabe 4:** Kopieren Sie die Definition der Funktion `square` und benennen Sie die Kopie in `polygon` um. Fügen Sie einen weiteren Parameter namens `n` hinzu und ändern Sie den Funktionsrumpf so, dass ein n-seitiges [reguläres Vieleck](https://de.wikipedia.org/wiki/Regelm%C3%A4%C3%9Figes_Polygon) (Polygon) gezeichnet wird. \n",
+ "\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-info\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Die Außenwinkel eines n-seitigen Vielecks betragen 360/n Grad.\n",
+ "\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "Versuchen Sie zunächst selber die Aufgabe zu lösen, anbei folgen ein paar Hinweise, die Sie verwenden können. \n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Für die Lösung müssen Sie eine Zeile Code hinzufügen und 2 Zeilen anpassen, überlegen Sie welche das sein könnten!\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Berechnen Sie den Seitenwinkel und speichern Sie ihn in einer Variable. Verändern Sie die Drehung so, dass Sie nicht immer 90° beträgt, sondern an den berechneten Winkel angepasst ist.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Für ein Polygon mit weniger als vier Seiten, ist es nicht so schlimm, wenn die Schildkröte eine Seite doppelt läuft, was ist aber mit den Formen, die mehr als vier Seiten haben?\n",
+ " \n",
+ " </div> \n",
+ "</details>"
]
},
{
@@ -502,11 +630,61 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.6 Schnittstellenentwurf\n",
+ "### Schnittstellenentwurf\n",
"\n",
"- **Aufgabe 5:** Schreiben Sie eine Funktion `circle`, die eine Schildkröte `t` und einen Radius `r` als Parameter erwartet und annähernd einen Kreis zeichnet, indem sie die Funktion `polygon` mit einer geeigneten Seitenlänge und Anzahl von Seiten aufruft. Testen Sie ihre Funktion mit verschiedenen Werten für `r`.\n",
"\n",
- " *(Hinweis: Finden Sie den Umfang des Kreises heraus und stellen Sie sicher, dass `length * n` gleich dem Umfang ist.)*"
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-info\"> Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Finden Sie den Umfang des Kreises heraus und stellen Sie sicher, dass `length * n` gleich dem Umfang ist. Die Formel für die Umfangsberechnung ist: $2 * π * r$\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "Wie gewohnt folgen nun einige Hinweise. Versuchen Sie zunächst die Aufgabe ohne Hilfe zu lösen.\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Schreiben Sie zunächst den Kopf der Funktion `circle'. Welche Parameter müssen der Funktion übergeben werden. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Anschließend können Sie sich mit dem Rumpf der Funktion `circle` beschäftigen. Hier wollen wir `polygon` aufrufen. Welche Informationen müssen Sie an `polygon` übergeben? Schauen Sie sich die Funktion an um rauszufinden, welche Parameter sie übergeben müssen. Überlegen Sie wie Sie aus den Parametern der Funktion `circle` die benötigten Werte berechnen können. \n",
+ " \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Berechnen Sie den Umfang des Kreises und legen Sie die Anzahl an Seiten fest, die Sie verwenden wollen. Wir schauen uns später an, wie Sie n in Abhängigkeit des Kreises berechnen können. Wenn Sie dafür eine Idee haben verwenden Sie diese gerne, ansonsten können Sie zunächst eine beliebige Anzahl an Seiten festlegen. (Wird diese Zahl zu groß, wird Python sehr langsam und stürzt eventuell ab, ist sie zu klein gewählt sieht der Kreis sehr eckig aus. Probieren Sie verschiedene Werte für n zwischen 0 und 80 und wählen Sie einen Wert, der Ihnen geeignet scheint.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Berechnen Sie die Länge jeder einzelnen Seite in Abhängigkeit vom Umfang und der Anzahl an Seiten indem Sie den Umfang durch die Anzahl an Seiten teilen\n",
+ " \n",
+ " </div> \n",
+ "</details>\n"
]
},
{
@@ -593,11 +771,11 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Jetzt ist die Anzahl der Liniensegmente eine ganze Zahl, die nah bei `Umfang/3` liegt, sodass die Länge jedes Segments ungefähr 3 beträgt. Das ist klein genug, damit der Kreis gut aussieht, aber auch groß genug, um eine effiziente Zeichnung zu ermöglichen und passt daher für jede Kreisgröße. \n",
+ "Jetzt ist die Anzahl der Liniensegmente eine ganze Zahl, die nah bei `Umfang/3` liegt, sodass die Länge jedes Segments ungefähr 1/3 beträgt. Das ist klein genug, damit der Kreis gut aussieht, aber auch groß genug, um eine effiziente Zeichnung zu ermöglichen und passt daher für jede Kreisgröße. \n",
"\n",
"Wir addieren 3, damit das Vieleck mindestens drei Seiten hat.\n",
"\n",
- "### 4.7 Refactoring\n",
+ "### Refactoring\n",
"\n",
"- **Aufgabe 6:** Schreiben Sie eine verallgemeinerte Funktion `circle`, die Sie `arc` nennen. Diese soll ein weiteres Argument `angle` erwarten, welches angibt, welcher Anteil des Kreises gezeichnet werden soll. Die Funktion `arc` soll also einen Kreisbogen zeichnen. Der Wert von `angle` ist dabei in Grad, so dass für `angle=360` ein vollständiger Kreis gezeichnet werden sollte.\n"
]
@@ -615,7 +793,51 @@
"source": [
"Als wir `circle` geschrieben haben, konnten wir `polygon` wiederverwenden, denn ein regelmäßiges Vieleck mit vielen Seiten ist eine gute Näherung für einen Kreis. Aber mit der Funktion `arc` klappt das nicht so einfach - wir können kein Vieleck und keinen Kreis nutzen, um einen Kreisbogen zu zeichnen.\n",
"\n",
- "Eine Alternative ist, mit einer Kopie von `polygon` zu beginnen und diese zu `arc` zu verändern. Das Ergebnis könnte so aussehen:\n",
+ "Eine Alternative ist, mit einer Kopie von `polygon` zu beginnen und diese zu `arc` zu verändern.\n",
+ "Hier finden Sie einige Hinweise wie Sie dabei vorgehen könnten:\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Schreiben Sie zunächst den Kopf der Funktion `arc'. Welche Parameter müssen der Funktion übergeben werden. Kopieren Sie den Rumpf von `polygon`damit Sie ihn sehen und verändern können. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Die Formel um die Länge eines Kreisbogens zu berechnen ist: $ 2 * π * r * Winkel / 360 \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Berechnen Sie n in Abhängigkeit des Umfangs, analog zu der Berechnung von n in `circle`. Berechnen Sie aus n und dem Umfang analog auch die Schrittlänge. \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Berechnen Sie den Winkel der Drehung in Abhängigkeit vom eingegebenen Winkel und der Anzahl an gemalten Abschnitten `n`. Nun sollten Sie alle notwendigen Zahlen haben, verwenden Sie diese für die Schleife, die in `polygon` geschrieben wurde.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "Das Ergebnis könnte dann so aussehen:\n",
"\n",
"\n",
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
@@ -752,7 +974,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.8 Ein Entwicklungsplan\n",
+ "## Ein Entwicklungsplan\n",
"\n",
"Ein **Entwicklungsplan** ist ein Prozess zum Schreiben von Programmen. Der Prozess, den wir in dieser Fallstudie verwendet haben, heißt \"Verkapselung und Verallgemeinerung\". Die Schritte dieses Prozesses sind:\n",
"\n",
@@ -770,7 +992,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.9 Docstring\n",
+ "## Docstring\n",
"\n",
"Ein **Docstring** ist eine Zeichenkette am Anfang einer Funktion, die die Schnittstelle der Funktion erklärt (\"doc\" ist kurz für \"documentation\", also Dokumentation). Hier ist ein Beispiel:"
]
@@ -812,7 +1034,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.10 Debugging\n",
+ "## Debugging\n",
"\n",
"Eine Schnittstelle ist wie ein Vertrag zwischen der Funktion und den Aufrufenden. Die Aufrufenden stimmen zu, bestimmte Parameter bereitzustellen und die Funktion stimmt zu, eine bestimmte Aufgabe zu erledigen.\n",
"\n",
@@ -833,7 +1055,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.11 Glossar\n",
+ "## Glossar\n",
"\n",
"Legen wir uns eine Liste mit den wichtigsten Begriffen an, die wir im Kapitel 4 gelernt haben:\n",
"\n",
@@ -856,13 +1078,13 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "### 4.12 Ãœbung\n",
+ "## Ãœbung\n",
"\n",
- "#### Aufgabe 1\n",
+ "### Aufgabe 1\n",
"\n",
- "Laden Sie den Code für dieses Kapitel [hier](http://thinkpython2.com/code/polygon.py) herunter.\n",
+ "Laden Sie den gesamten Code für dieses Kapitel [hier](http://thinkpython2.com/code/polygon.py) herunter. Dieser Code ist weitestgehend deckungsgleich mit dem Code, den wir in diesem Kapitel angesehen haben, kann aber sehr hilfreich sein, wenn Sie nicht in Jupyter Notebooks arbeiten können. \n",
"\n",
- "*Hinweis: Um Probleme mit Turtle+Jupyter zu vermeiden, stellen Sie sicher, dass am Ende Ihres Programmes stets die folgenden beiden Zeilen stehen:*"
+ "Um Probleme mit Turtle+Jupyter zu vermeiden, stellen Sie sicher, dass am Ende Ihres Programmes stets die folgenden beiden Zeilen stehen:"
]
},
{
@@ -887,13 +1109,129 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "#### Aufgabe 2\n",
+ "### Aufgabe 2\n",
"\n",
"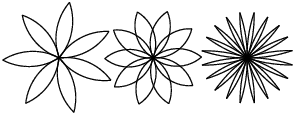\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Blumen.\n",
"\n",
- "*(Die Lösung benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py).)*\n"
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-info\">Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Die Lösung benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py). \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Wenn Sie sich die Blume ansehen, können Sie feststellen, dass zwei Teile ineinander greifen um die Blume zu erzeugen. Welche Teile sind das?\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Die Blütenblätter werden einzeln hintereinander gezeichnet, konzentrieren Sie sich also zuerst darauf, ein einzelnes Blütenblatt zu zeichnen.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Überlegen Sie wie der Kopf der Blütenblattfunktion aussehen muss und schreiben Sie diese. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Sie müssen der Funktion eine Schildkröte übergeben, die das Blatt zeichnen soll. Die Funktion braucht auch den Radius des Kreisbogens, welcher die Länge des Blatts bestimmt und den Winkel in dem das Blatt gezeichnet werden soll und damit wie breit des Blütenblatt wird.\n",
+ "\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Wie im vorherigen Hinweis schon angesprochen besteht das Blütenblatt aus 2 Kreisbögen. Verwenden Sie eine Schleife und `arc` um das Blatt zu zeichnen. Vergessen Sie nicht, die Funktion zu testen. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Nach dem ersten Kreisbogen muss die Schildkröte sich soweit drehen, dass sie mit dem nächsten Kreisbogen eine volle 180° Drehung vollzogen hat.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Wenn Sie ein einzelnes Blütenblatt zeichnen können gilt es nun sich zu überlegen, wie man die Blütenblätter zu einer Blume zusammenfügen kann. Schreiben Sie den Kopf der Blumen Funktion und überlegen Sie, welche Informationen der Funktion übergeben werden müssen\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Da die Blumenfunktion Informationen an die Blütenblatt Funktion weitergeben muss, muss die Funktion die selben Parameter erhalten. Zusätzlich muss die Funktion noch gesagt bekommen, wie viele Blütenblätter gezeichnet werden sollen.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Um die richtige Anzahl an Blütenblättern zu zeichnen müssen Sie die Funktion \"Blatt\" innerhalb der Funktion \"Blume\" entsprechend oft aufrufen, verwenden Sie dafür eine Schleife.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Um die Blütenblätter gleichmäßig um den Mittelpunkt der Blume zu verteilen, muss der Winkel zwischen den Blättern so berechnet werden, dass nach Vollenden der Blume eine 360° Wendung vollzogen wurde. Überlegen Sie wie Sie dabei vorgehen müssen?\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">11. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Dafür muss der Winkel zwischen den Blättern 360/n betragen, wobei n für die Anzahl der Blätter steht.\n",
+ "\n",
+ " </div> \n",
+ "</details>"
]
},
{
@@ -913,20 +1251,8 @@
"\n",
"(Quelle: Jason Eppink, Flickr)\n",
"\n",
- "1. Die Blumen bestehen aus 2 Teilen.... \n",
- "2. Überlegen Sie erst, wie man ein einzelnes Blütenblatt zeichnen kann.\n",
- "3. Welche Informationen müssen der Funktion in der Schnittstelle übergeben werden?\n",
- "4. Die Funktion braucht eine Schildkröte, die Größe des Blütenblatts und Winkel in dem das Blütenblatt gezeichnet werden soll (also wie breit das Blütenblatt sein soll)\n",
- "3. Jedes Blütenblatt besteht aus 2 Kreisbögen, also brauchen Sie arc (nutzen Sie ihre eigene Funktion oder kopieren Sie arc aus polygon.py)\n",
- "4. Nach dem ersten Kreisbogen muss die Schildkröte sich soweit drehen, dass sie mit dem nächsten Kreisbogen eine volle 180° Drehung vollzogen hat\n",
- "5. Wie können sie die Blütenblätter dann miteinander zu einer blume verbinden?\n",
- "8. Was muss der Funktion Blume in der Schnittstelle an Argumenten übergeben werden? \n",
- "9. Sie brauchen alle Argumente, die in der Funktion an Blatt übergeben werden und natürlich auch die Anzahl n an Blütenblättern, aus denen die Blume bestehen soll.\n",
- "6. In Blume muss Blatt n mal aufgerufen werden \n",
- "6. Um die Blütenblätter gleichmäßig um den Mittelpunkt der Blume zu verteilen, muss der Winkel zwischen den Blättern so berechnet werden, dass nach Vollenden der Blume eine 360° Wendung vollzogen wurde.\n",
- "7. Dafür muss der Winkel zwischen den Blättern 360/n betragen\n",
"\n",
- "Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/flower.py)"
+ "Hier ist eine weitere mögliche [Lösung](http://thinkpython2.com/code/flower.py)"
]
},
{
@@ -962,12 +1288,110 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "#### Aufgabe 3\n",
+ "### Aufgabe 3\n",
"\n",
"\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Figuren.\n",
- "\n"
+ "\n",
+ "\n",
+ "Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Wir gehen analog zu Blume vor, und zeichnen die einzelnen \"Kuchenstücke\" bevor wir sie zu dem \"Kuchen\" zusammensetzen.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Erzeugen Sie zunächst den Kopf der Funktion für ein einzelnes Kuchenstück. Überlegen Sie anschließend, wie Sie das Dreieck zeichnen könnten. Welche Informationen müssen dem Kopf der Funktion übergeben werden?\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Die Funktion für das Kuchenstück muss die Schildkröte, die Seitenlänge (die der Radius der Form \"Kuchen ist, daher nennen wir sie \"r\") und den Winkel übergeben bekommen, in dem das Kuchenstück gezeichnet werden soll. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Da wir die beiden Seitenlängen vorgeben, müssen wir die obere Länge in Abhängigkeit von den Seitenlängen (dem Radius der Form Kuchen und dem Winkel berechnen. Wir verwenden das sogenannte Bogenmaß. Die vollständige dafür Formel ist $2*r*sin(angle*\\pi/180)$ \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Um Herauszufinden, wie weit sich die Schildkröte drehen muss, ist es am Einfachsten verschiedene Drehwinkel auszuprobieren, bis es funktioniert. Verwenden Sie 90 Winkel als Basis und addieren oder subtrahieren Sie den Winkel aus dem Funktionskopf\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Damit die Schildkröte den gesamten Kuchen zeichnen kann muss Sie immer in derselben Position starten und enden. Dafür muss Sie sich zu Beginn im angegebenen Winkel drehen und am Ende soweit, dass sie wieder die Ausgangsposition annimmt. Um die Position wieder anzunehmen muss sich die Schildkröte um weniger als 180 Grad drehen. Der genaue Winkel kann mit Hilfe des Winkel-Parameters berechnet werden. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Um die Kuchen-Funktion zu schreiben können Sie die Blume-Funktion kopieren und anpassen. Es müssen einige Veränderungen vorgenommen werden. Überlegen Sie welche Änderungen das sind. Um einen Eindruck zu bekommen, können Sie Kuchen aufrufen und sehen welche Fehler auftreten.\n",
+ "\n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Damit der Kuchen ohne Lücken gezeichnet werden kann muss der Winkel berechnet werden und nicht der Funktion übergeben werden. Im Funktionskopf muss also nur der Radius der Figur, also die Seitenlänge der einzelnen Stücke, die Schildkröte und die Anzahl der Stücke übergeben werden. Der Winkel wird dann in Abhängigkeit von der Anzahl der Stücke berechnet.\n",
+ "\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ "\n",
+ "Der Winkel zwischen den Stücken ist, da wir eine volle Drehung vornehmen wollen 360 geteilt durch die Anzahl der Stücke. In der Schleife rufen wir Stück auf, dort müssen wir den Winkel anpassen, bevor wir die entsprechende Drehung vornehmen. Führen Sie die Funktion aus und versuchen Sie herauszufinden, wie Sie den Winkel in stück anpassen müssen.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Der Winkel für Stück ist der halbe Winkel zwischen Stücken. Wir nehmen also die Winkelvariable/2 als zu übergebenden Wert.\n",
+ "\n",
+ " </div> \n",
+ "</details>\n"
]
},
{
@@ -986,16 +1410,6 @@
"\n",
"(Quelle: Jason Eppink, Flickr)\n",
"\n",
- "1. Wir gehen analog zu Blume vor, und zeichnen die einzelnen \"Kuchenstücke\" bevor wir sie zu dem \"Kuchen\" zusammensetzen.\n",
- "2. Wir müssen die obere Seitenlänge berechnen um sie zeichnen zu können. Sinus verwendet Bogenmaß, das heißt um die \"richtige\" Seitenlänge zu erhalten müssen wir den Winkel umrechnen. *Hinweiß: Dafür wird mit $\\pi/180$ multipliziert*\n",
- "3. Die vollständige Formel ist $2*r*sin(angle*\\pi/180)$ \n",
- "4. Über die 3 Seiten verteilt, muss sich die Schildkröte soweit drehen, dass sie wieder am Ausgangspunkt ankommen. \n",
- "5. Sie muss zweimal die Strecke r laufen und dazwischen einmal die Strecke, die wir berechnet haben.\n",
- "6. Dazwischen muss sich die Schildkröte immer drehen. Verwenden Sie dafür angle und Vielfältige von 90 und probieren Sie verschiedene Varienten aus, bis es funktioniert.\n",
- "7. Damit kuchen später funktioniert, muss die Schildkröte wieder ihre Ausgangsposition Annehmen. Dafür fügen Sie noch je eine Drehung am Anfang und am Ende ein.\n",
- "8. Für kuchen können Sie blume wiederverwenden, müssen allerdings einige Veränderungen vornehmen. Damit keine Lücken entstehen, muss die Funktion angle berechnen, statt diesen Wert übergehen zu bekommen. Dann muss auch der Winkel für Stück angepasst werden.\n",
- "9. Um die Stücke zu verbinden wird in der for Schleife eine Drehung von 360/n vorgenommen. Die Drehung in Stück muss dann halb so groß sein. \n",
- "\n",
"*(Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/pie.py))*"
]
},
@@ -1041,10 +1455,67 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "#### Aufgabe 4\n",
- "\n",
- "\n",
- "Lesen Sie etwas zu Spiralen auf [Wikipedia](https://de.wikipedia.org/wiki/Spirale). Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n"
+ "### Aufgabe 4\n",
+ "\n",
+ "\n",
+ "Lesen Sie etwas zu Spiralen auf [Wikipedia](https://de.wikipedia.org/wiki/Spirale). Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "In dieser Aufgabe, können Sie entscheiden, wie komplex Sie die Schnittstelle gestalten wollen. Sie müssen mindestens die Schildkröte übergeben, die die Spirale zeichnen soll, in maximaler Komplexität kann der Nutzer alle Variablen der Spirale anpassen. Hier wurde entschieden, dass der Nutzer lediglich die Schildkröte und die Anzahl der Spiralensegmente angeben darf, wenn Sie eine komplexere Lösung haben wollen, fügen Sie diese Parameter dem Funktionsaufruf hinzu.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Die Formel für die Berechnung von Spiralen ist $r = a + b*\\theta$. Dabei können Sie einfach Ausgangswerte für a und b festlegen. Ein geeigneter Wert für a ist zum Beispiel 0.1 und für b 0.0002. Wenn ihre Funktion funktioniert, probieren Sie verschiedene Werte für a und b aus und sehen Sie sich an, wie die Spirale sich verändert. \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Weitere Parameter können entweder in der Schnittstelle oder aber wie in dem Beispiel unten in der Funktion festgelegt werden. Diese Parameter sind der Ausgangswinkel theta der Spirale und die Länge der einzelnen Spiralensegmente.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Analog zum Kreisbogen wird auch die Spirale durch kurze gerade Segmente und Drehungen gezeichnet. Da das Zeichnen von Segmenten n-mal wiederholt wird, benötigen Sie eine for-Schleife.\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "In der Schleife muss für jedes Segment neu berechnet werden wie weit die Schildkröte sich drehen muss, da der Winkel nicht konstant bleibt. Dafür verwendet die Lösung: dtheta = 1 / (a + b * theta)\n",
+ " \n",
+ " </div> \n",
+ "</details>\n",
+ "\n",
+ "\n",
+ "<details>\n",
+ " <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
+ " <div class=\"alert alert-info\" role=\"alert\">\n",
+ " \n",
+ "Da diese Formel theta als den Winkel des vorherigen Abschnitts verwendet, muss theta ebenfalls in jedem Schleifendurchlauf überschrieben werden - also addieren Sie dtheta auf theta auf. \n",
+ " \n",
+ " </div> \n",
+ "</details>\n"
]
},
{
@@ -1060,15 +1531,6 @@
"source": [
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
"\n",
- "1. Sie müssen sich entscheiden, welche Argumente Sie in der Schnittstelle übergeben wollen und welche Sie der Funktion übergeben wollen. (Hier habe ich mich entschieden, Nutzern verschiedene funktionierende Schleifen zur Auswahl zu geben)\n",
- "2. In einem minimalistischen Schnittstellen Entwurf muss noch mindestens die Schildkröte an die Funktion übergeben werden.\n",
- "3. Die Formel für die Berechnung von Spiralen ist $r = a + b\\theta$ , a können Sie auf 0.1 und b auf 0.0002 als Ausgangswerte festlegen. \n",
- "4. Andere Parameterm die Sie entweder in der Schnittstelle oder in der Funktion festlegen müssen sind der Winkel theta, die Anzahl an Spiralensegmenten und die Länge der einzelnen Segmente. \n",
- "5. Analog zum Kreisbogen wird auch die Spirale durch kurze gerade Segmente und Drehungen gezeichnet. Da das Zeichnen von Segmenten n-mal wiederholt wird, benötigen Sie eine for-Schleife.\n",
- "6. In der Schleife muss für jedes Segment neu berechnet werden wie weit die Schildkröte sich drehen muss, da der Winkel nicht konstant bleibt. Dafür verwendet die Lösung: dtheta = 1 / (a + b * theta)\n",
- "7. Da diese Formel theta als den Winkel des vorherigen Abschnitts verwendet, muss theta ebenfalls in jedem Schleifendurchlauf überschrieben werden - also addieren Sie dtheta auf theta auf. \n",
- " \n",
- "\n",
"\n",
"Eine [Lösung](http://thinkpython2.com/code/spiral.py)"
]
@@ -1105,7 +1567,7 @@
"metadata": {},
"source": [
"\n",
- "#### Aufgabe 5\n",
+ "### Aufgabe 5\n",
"\n",
"*(Hinweis: Dies ist eher eine Fleiß- und Zusatzaufgabe.)*\n",
"\n",
--
GitLab