From fdc46262367c565832e96e40874a0d3845ed1953 Mon Sep 17 00:00:00 2001
From: =?UTF-8?q?Robert=20J=C3=A4schke?= <jaeschke@l3s.de>
Date: Mon, 6 Nov 2017 09:23:10 +0000
Subject: [PATCH] 3. Teil fertig
---
notebooks/seminar03.ipynb | 372 ++++++++++++++++++++++++++++++++------
1 file changed, 320 insertions(+), 52 deletions(-)
diff --git a/notebooks/seminar03.ipynb b/notebooks/seminar03.ipynb
index 78f0493..77ceb90 100644
--- a/notebooks/seminar03.ipynb
+++ b/notebooks/seminar03.ipynb
@@ -17,7 +17,9 @@
"\n",
"## Exkurs: Was mir an Python gefällt\n",
"\n",
- "In dieser Rubrik, die immer am Anfang eines Kapitels steht, möchte ich Ihnen zeigen, wofür ich Python nutze und warum ich es mag. Sie werden vielleicht noch nicht verstehen, was ich genau mache, aber Sie sehen damit schon einmal die Möglichkeiten von Python und können später darauf zurückgreifen. Da dies auch ein Exkurs ist, können Sie diese Rubrik gerne auch erst einmal überspringen."
+ "In dieser Rubrik, die immer am Anfang eines Kapitels steht, möchte ich Ihnen zeigen, wofür ich Python nutze und warum ich es mag. Sie werden vielleicht noch nicht verstehen, was ich genau mache, aber Sie sehen damit schon einmal die Möglichkeiten von Python und können später darauf zurückgreifen. Da dies auch ein Exkurs ist, können Sie diese Rubrik gerne auch erst einmal überspringen.\n",
+ "\n",
+ "Es ist sehr leicht, Ergebnisse mit Hilfe eines Plots darzustellen und auch mathematische Funktionen können professionell geplottet werden:"
]
},
{
@@ -27,12 +29,17 @@
"outputs": [],
"source": [
"%matplotlib inline\n",
- "import random, math\n",
+ "import math\n",
"import matplotlib.pyplot as pyplot\n",
"\n",
- "random.random()\n",
- "\n",
- "pyplot.plot(range(1,4), range(2,5))"
+ "# sin(x) und cos(x) zwischen 0 und 2pi\n",
+ "x = [xx/10 for xx in range(0,int(2*math.pi*10))]\n",
+ "sinx = [math.sin(xx) for xx in x]\n",
+ "cosx = [math.cos(xx) for xx in x]\n",
+ "pyplot.plot(x, sinx, label='sin(x)')\n",
+ "pyplot.plot(x, cosx, label='cos(x)')\n",
+ "pyplot.grid(linestyle=\"dashed\")\n",
+ "pyplot.legend()"
]
},
{
@@ -45,23 +52,23 @@
"\n",
"### Warum?\n",
"\n",
- "- Lesbarkeit\n",
- "- Fehlersuche\n",
- "- kürzerer Programmkode\n",
- "- Wartbarkeit\n",
- "- Testbarkeit\n",
- "- Wiederverwendbarkeit\n",
- "\n",
- "It may not be clear why it is worth the trouble to divide a program into functions. There are several reasons:\n",
- "\n",
- " Creating a new function gives you an opportunity to name a group of statements, which makes your program easier to read and debug.\n",
- " Functions can make a program smaller by eliminating repetitive code. Later, if you make a change, you only have to make it in one place.\n",
- " Dividing a long program into functions allows you to debug the parts one at a time and then assemble them into a working whole.\n",
- " Well-designed functions are often useful for many programs. Once you write and debug one, you can reuse it.\n",
+ "Warum ist es sinnvoll, ein Programm in Funktionen aufzuteilen?\n",
"\n",
+ "- **Lesbarkeit** - z.B. weil eine Folge von Anweisungen dann einen Namen trägt der beschreibt, was sie tun\n",
+ "- **Fehlersuche** - z.B. weil Fehler innerhalb einer Funktion den Suchbereich einschränken \n",
+ "- **kürzerer Programmkode** - z.B. weil sich Quellcode nicht wiederholt\n",
+ "- **Wartbarkeit** - z.B. weil wir Änderungen nur an einer Stelle durchführen müssen\n",
+ "- **Testbarkeit** - z.B. wir jede Funktion einzeln testen können\n",
+ "- **Wiederverwendbarkeit** - weil eine gut funktionierende Funktion in vielen Programmen verwendet werden kann."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
"### Funktionsaufrufe\n",
"\n",
- "Wir haben schon einige Funktionsaufrufe gesehen:\n"
+ "Wir haben schon einige Funktionsaufrufe gesehen:"
]
},
{
@@ -81,7 +88,7 @@
"\n",
"Üblicherweise sagen wir, dass eine Funktion ein Argument \"erwartet\" und ein Ergebnis \"zurückgibt\". Dieses Ergebnis wird auch **Rückgabewert** genannt. \n",
"\n",
- "Python stellt einige Funktionen bereit, um Werte von einem Datentyp zu einem anderen umzuwandeln. Beispielsweise wandelt erwartet die `int`-Funktion einen Wert als Argument, den sie dann in eine ganze Zahl umwandelt - falls möglich (andernfalls beschwert sie sich und gibt einen Fehler aus):"
+ "Python stellt einige Funktionen bereit, um Werte von einem Datentyp zu einem anderen umzuwandeln. Beispielsweise erwartet die `int`-Funktion einen Wert als Argument, den sie dann in eine ganze Zahl umwandelt - falls möglich (andernfalls beschwert sie sich und gibt einen Fehler aus):"
]
},
{
@@ -240,7 +247,23 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Darin sind Funktionen und Variablen enthalten, die in der Moduldatei definiert wurden. Um auf eine der Funktionen oder Variablen zuzugreifen, müssen wir den Namen des Moduls angeben und den Namen der Funktion (oder Variable), getrennt durch einen Punkt:"
+ "Hilfreicher ist es allerdings, das Modulobjekt der Funktion `help` zu übergeben: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "help(math)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Im Modulobjekt sind Funktionen und Variablen enthalten, die in der Moduldatei definiert wurden. Um auf eine der Funktionen oder Variablen zuzugreifen, müssen wir den Namen des Moduls angeben und den Namen der Funktion (oder Variable), getrennt durch einen Punkt:"
]
},
{
@@ -256,7 +279,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Dies gibt beispielsweise den Wert der Sinus-Funktion an der Stelle 3 aus. Dieses Format heißt **Punkt-Schreibweise** (Englisch: /dot notation/) und wird uns öfter begegnen.\n",
+ "Dies gibt beispielsweise den Wert der Sinus-Funktion an der Stelle 3 aus. Dieses Format heißt **Punkt-Schreibweise** (Englisch: *dot notation*) und wird uns öfter begegnen.\n",
"\n",
"Ein weiteres Beispiel ist der Wert von π, der im `math`-Modul definiert ist: "
]
@@ -274,7 +297,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Der Wert ist in der Variable `pi` im `math`-Modul definiert, auf die wir mit Hilfe der Punkt-Schreibweise zugreifen können."
+ "Der Wert ist in der Variablen `pi` im `math`-Modul definiert, auf die wir mit Hilfe der Punkt-Schreibweise zugreifen können."
]
},
{
@@ -283,7 +306,7 @@
"source": [
"### Verknüpfung\n",
"\n",
- "Bisher haben wir uns die Elemente von Programmen -- Variablen, Ausdrücke, Anweisungen -- einzeln angeschaut aber nicht groß darüber gesprochen, wie wir sie kombinieren können. \n",
+ "Bisher haben wir uns die Elemente von Programmen - Variablen, Ausdrücke, Anweisungen - einzeln angeschaut aber nicht groß darüber gesprochen, wie wir sie kombinieren können. \n",
"\n",
"Eine der nützlichsten Eigenschaften von Programmiersprachen ist, dass wir kleinere Bausteine miteinander **verknüpfen** (Englisch: *compose*/*composition*) können. Beispielsweise kann das Argument einer Funktion jeglicher Ausdruck sein, einschließlich arithmetischer Operatoren"
]
@@ -329,10 +352,8 @@
"source": []
},
{
- "cell_type": "code",
- "execution_count": null,
+ "cell_type": "markdown",
"metadata": {},
- "outputs": [],
"source": [
"Fast überall, wo wir einen Wert verwenden können, können wir auch einen beliebigen Ausdruck einsetzen:"
]
@@ -344,7 +365,7 @@
"outputs": [],
"source": [
"gesamt = degrees * 20 # richtig\n",
- "20 * degrees = gesamt # falsch!\n"
+ "20 * degrees = gesamt # falsch!"
]
},
{
@@ -385,7 +406,7 @@
"- Danach kommt der **Rumpf** (Englisch: *body*), der um vier Leerzeichen eingerückt werden muss.\n",
"- Im Rumpf können beliebig viele Anweisungen stehen ... die erste Anweisung, die nicht mehr eingerückt ist, gehört nicht mehr zur Funktion.\n",
"\n",
- "Wenn wir das alles beachtet und richtig gemacht haben (was am Anfang wohl kompliziert aussieht), dann können wir die Funktion aufrufen:"
+ "Wenn wir das alles beachtet und richtig gemacht haben, dann können wir die Funktion aufrufen:"
]
},
{
@@ -421,7 +442,7 @@
"source": [
"Das Objekt trägt den Namen der Funktion und ist vom Typ `function`. \n",
"\n",
- "Sobald wir eine Funktion definiert haben, können wir diese in anderen Funktionen verwenden. Wir könnten zum Beispiel eine Funktion schreiben, die unsere `print_lyrics`-Funktion zweimal aufruft. Implementieren Sie diese Funktion:"
+ "Sobald wir eine Funktion definiert haben, können wir diese in anderen Funktionen verwenden. Wir könnten zum Beispiel eine Funktion `repeat_lyrics` schreiben, die unsere `print_lyrics`-Funktion zweimal aufruft. Implementieren Sie diese Funktion:"
]
},
{
@@ -472,7 +493,7 @@
"\n",
"Vielleicht haben Sie es sich schon gedacht: Bevor wir eine Funktion nutzen können, müssen wir sie definieren. Die Funktionsdefinition muss also *vor* dem Funktionsaufruf ausgeführt werden.\n",
"\n",
- "Daher als Ãœbung: verschieben Sie den Funktionsaufruf in der letzten Zeile ganz an den Anfang, so dass der Funktionsaufuruf vor den Funktionsdefinitionen erscheint und beobachten Sie^, welche Fehlermeldung das ergibt:"
+ "Daher als Ãœbung: verschieben Sie den Funktionsaufruf in der letzten Zeile ganz an den Anfang, so dass der Funktionsaufuruf vor den Funktionsdefinitionen erscheint und beobachten Sie, welche Fehlermeldung das ergibt:"
]
},
{
@@ -505,7 +526,7 @@
"source": [
"### Kontrollfluss\n",
"\n",
- "Damit wir sicherstellen können, dass eine Funktion definiert ist, bevor wir sie aufrufen, müssen wir die Reihenfolge kennen, in der Anweisungen ausgeführt werden -- den sogenannten **Kontrollfluss*.\n",
+ "Damit wir sicherstellen können, dass eine Funktion definiert ist, bevor wir sie aufrufen, müssen wir die Reihenfolge kennen, in der Anweisungen ausgeführt werden - den sogenannten **Kontrollfluss**.\n",
"\n",
"Die Ausführung eines Programms beginnt immer mit der ersten Anweisung. Anweisungen werden einzeln ausgeführt, von oben nach unten.\n",
"\n",
@@ -515,9 +536,9 @@
"\n",
"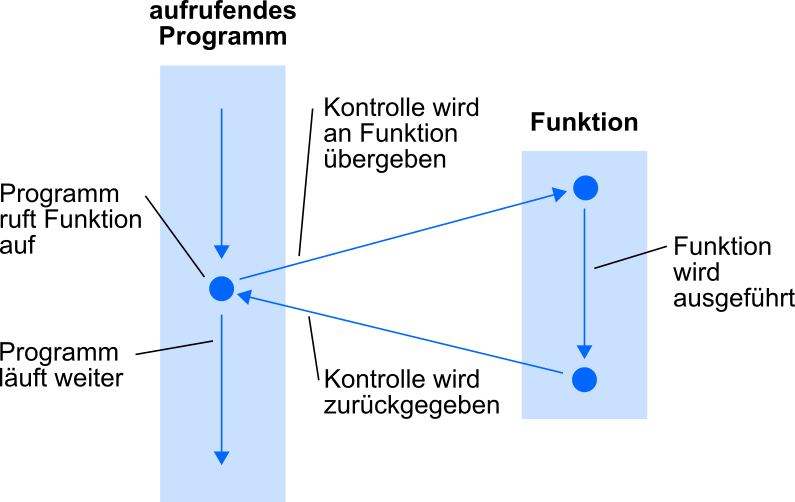\n",
"\n",
- "Das klingt noch recht einfach ... aber wir erinnern uns: eine Funktion kann eine weitere aufrufen und diese noch eine weitere, usw. Glücklicherweise merkt sich Python immer genau, wo es ist und wo zurückgesprungen werden muss. \n",
+ "Das klingt noch recht einfach ... aber wir erinnern uns: eine Funktion kann eine weitere aufrufen und diese noch eine weitere, usw. Glücklicherweise merkt sich Python immer genau, wo es ist und wohin zurückgesprungen werden muss. \n",
"\n",
- "Wenn wir also ein Programm zu verstehen versuchen, ist es manchmal hilfreich, nicht einfach nur von oben nach unten durchzulesen, sondern dem Kontrollfluss zu folgen, also beim Aufruf einer Funktion zu dieser Funktion zu springen und sie durchzulesen."
+ "Wenn wir also ein Programm zu verstehen versuchen, ist es manchmal hilfreich, das Programm nicht einfach nur von oben nach unten durchzulesen, sondern dem Kontrollfluss zu folgen, also beim Aufruf einer Funktion zu dieser Funktion zu springen und sie durchzulesen."
]
},
{
@@ -602,7 +623,7 @@
"metadata": {},
"source": [
"**Wichtig**: der Name der Variablen, die wir als Argument übergeben (hier: `text`) hat nichts mit dem Namen des Parameters (hier `wert`) zu tun! Egal, wie der Wert der da reinkommt ausserhalb der Funktion bezeichnet wurde -\n",
- "- innerhalb dieser Funktion heißt der Wert `wert`."
+ " innerhalb dieser Funktion heißt der Wert `wert`."
]
},
{
@@ -663,7 +684,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Parameter sind auch lokal. Außerhalb von `print_twice` können wir nicht auf `wert` zugreifen:"
+ "Parameter sind auch lokal. Außerhalb von `cat_twice` können wir auf `part1` nicht zugreifen:"
]
},
{
@@ -672,7 +693,7 @@
"metadata": {},
"outputs": [],
"source": [
- "print(wert)"
+ "print(part1)"
]
},
{
@@ -687,9 +708,9 @@
"\n",
"Das Diagramm zeigt uns den Wert jeder Variablen und auch die Funktion zu der jede Variable gehört.\n",
"\n",
- "Jede Funktion wird durch eine **Box** (Englisch: *frame*) repräsentiert: links neben der Box erscheint der Name der Funktion und innerhalb der Box die Parameter und Variablen und die Werte, die ihnen zugewiesen wurden.\n",
+ "Jede Funktion wird durch einen **Block** (Englisch: *frame*) repräsentiert: links neben dem Block erscheint der Name der Funktion und innerhalb des Blocks die Parameter und Variablen und die Werte, die ihnen zugewiesen wurden.\n",
"\n",
- "Die Boxen sind in einem Stapel (*stack*) angeordnet, der uns zeigt, welche Funktion welche andere Funktion aufgerufen hat. In unserem Beispiel wurde `print_twice` durch `cat_twice` aufgerufen und `cat_twice` wurde durch `__main__` aufgerufen, was ein spezieller Name für die oberste Box ist. Wenn wir eine Variable ausserhalb einer Funktion erzeugen, gehört diese zu `__main__`.\n",
+ "Die Blöcke sind in einem Stapel (*stack*) angeordnet, der uns zeigt, welche Funktion welche andere Funktion aufgerufen hat. In unserem Beispiel wurde `print_twice` durch `cat_twice` aufgerufen und `cat_twice` wurde durch `__main__` aufgerufen, was ein spezieller Name für den obersten Block ist. Wenn wir eine Variable ausserhalb einer Funktion erzeugen, gehört diese zu `__main__`.\n",
"\n",
"Jeder Parameter verweist auf den selben Wert wie das zugehörige Argument. In unserem Fall hat also `part1` den selben Wert wie `teil1`, `part2` den selben Wert wie `teil2` und `wert` den selben Wert wie `cat`.\n",
"\n",
@@ -796,7 +817,21 @@
"source": [
"Aber wenn wir sonst nichts damit machen, dann geht der Wert verloren. Wir berechnen also etwas, aber fangen damit nichts weiter an. Daher weisen wir den Rückgabewert einer Funktion meist einer Variablen zu oder verwenden ihn in einem Ausdruck, wie oben gesehen.\n",
"\n",
- "Funktionen ohne Rückgabewert zeigen vielleicht etwas auf dem Bildschirm an oder haben einen anderen Effekt, aber sie geben uns keinen Wert zurück. Wenn wir das Ergebnis einer solchen Funktion einer Variablen zuweisen, erhält diese den speziellen Wert `None`:\n"
+ "Schreiben Sie einen Ausdruck auf, der die Funktion `math.sqrt` verwendet und weisen Sie das Ergebnis einer Variablen zu:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Funktionen ohne Rückgabewert zeigen vielleicht etwas auf dem Bildschirm an oder haben einen anderen Effekt, aber sie geben uns keinen Wert zurück. Wenn wir das Ergebnis einer solchen Funktion einer Variablen zuweisen, erhält diese den speziellen Wert `None`:"
]
},
{
@@ -849,7 +884,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "Diese Funktion erhält als Argument einen Wert, der dem Parameter `radius` zugewiesen wird. Innerhalb wird dieser Wert verwendet, um eine Berechnung durchzuführen. Das Ergebnis der Berechnung wird der lokalen Variablen `a` zugewiesen, die schließlich in der letzten Zeile mittels `return a` zurückgegeben wird. Wenn wir jetzt die Funktion aufrufen, erhalten wir einen Wert zurück:"
+ "Diese Funktion erhält als Argument einen Wert, der dem Parameter `radius` zugewiesen wird. Innerhalb der Funktion wird dieser Wert verwendet, um eine Berechnung durchzuführen. Das Ergebnis der Berechnung wird der lokalen Variablen `a` zugewiesen, die schließlich in der letzten Zeile mittels `return a` zurückgegeben wird. Wenn wir jetzt die Funktion aufrufen, erhalten wir einen Wert zurück:"
]
},
{
@@ -879,10 +914,14 @@
"\n",
"Debugging ist wie Detektiv spielen: Wir haben ein paar Hinweise und wir müssen die Vorgänge und Ereignisse herausfinden, die zu den Ergebnissen geführt haben, die wir sehen.\n",
"\n",
- "Debugging ist aber auch wie experimentelle Wissenschaft: Wenn wir erstmal eine Idee haben, was schiefgelaufen sein könnte, können wir unser Programm verändern und es noch einmal versuchen. Wenn unsere Annahme richtig war, können wir das Ergebnis unserer Veränderung vorhersagen und mit dem realen Ergebnis vergleichen. Damit kommen wir hoffentlich einem richtig funktionierendem Programm näher. Wenn unsere Annahme falsch war, müssen wir uns eine neue Ausdenken. Wie schon Sherlock Holmes sagte: \"Wenn man das Unmögliche ausgeschlossen hat, muss das, was übrig bleibt - wie wie unwahrscheinlich auch immer - die Wahrheit sein\" (A. Conan Doyle, *The Sign of Four*).\n",
+ "\n",
+ "\n",
+ "Debugging ist aber auch wie experimentelle Wissenschaft: Wenn wir erstmal eine Idee haben, was schiefgelaufen sein könnte, können wir unser Programm verändern und es noch einmal versuchen. Wenn unsere Annahme richtig war, können wir das Ergebnis unserer Veränderung vorhersagen und mit dem realen Ergebnis vergleichen. Damit kommen wir hoffentlich einem richtig funktionierendem Programm näher. Wenn unsere Annahme falsch war, müssen wir uns eine neue Ausdenken. Wie schon Sherlock Holmes sagte: \"Wenn man das Unmögliche ausgeschlossen hat, muss das, was übrig bleibt - wie unwahrscheinlich auch immer - die Wahrheit sein\" (A. Conan Doyle, *The Sign of Four*).\n",
"\n",
"Für viele Menschen ist Programmieren und Debugging das gleiche. D.h., Programmieren bedeutet, dass man ein Programm solange debuggt, bis es das tut, was man möchte. Die Idee ist, dass man mit einem kleinen, einfachen Programm beginnt und solange kleine Änderungen vornimmt und debuggt, bis es tut was es soll.\n",
"\n",
+ "\n",
+ "\n",
"Zum Beispiel ist Linux ein Betriebssystem, was auf Millionen von Rechnern verwendet wird und Millionen von Codezeilen enthält, aber es begann als ein einfaches Programm welches der finnische Student Linus Torvalds geschrieben hat, um den Intel 386 Prozessor besser zu verstehen. Laut Larry Greenfield war einer der ersten Versuche von Linus ein Programm, welches abwechselnd \"AAAA\" und \"BBBB\" ausgab. Daraus wurde später Linux. (*The Linux Users’ Guide Beta Version 1*). "
]
},
@@ -925,7 +964,7 @@
"\n",
"### Aufgabe 1\n",
"Diese Aufgabe kennen Sie schon vom Seminar letzte Woche. Sie haben drei Möglichkeiten:\n",
- "1. Ãœbersprinen Sie die Aufgabe, weil Sie verstanden haben, wie alles funktioniert.\n",
+ "1. Ãœberspringen Sie die Aufgabe, weil Sie verstanden haben, wie alles funktioniert.\n",
"2. Lösen Sie die Aufgabe selbständig.\n",
"3. Scrollen Sie etwas herunter und lösen Sie die Aufgabe mit etwas Hilfe (\"Lückentext\").\n",
"\n",
@@ -956,9 +995,8 @@
"outputs": [],
"source": [
"# Wenn Sie fertig sind, rufen Sie die Funktion hier auf:\n",
- "right_justify('monty')\n",
- "right_justify('python')\n",
- "right_justify('life of Brian')\n",
+ "right_justify(\"Monty Python's\")\n",
+ "right_justify('The Ministry of Silly Walks')\n",
"# (und testen Sie die Funktion zwischendurch immer mal)"
]
},
@@ -966,6 +1004,8 @@
"cell_type": "markdown",
"metadata": {},
"source": [
+ "\n",
+ "\n",
"Bitte hier nur weiterlesen, wenn Sie Hilfe benötigen. Versuchen Sie es aber vorher unbedingt erst einmal zu zweit. Das Erfolgserlebnis, die Lösung selber gefunden zu haben, lohnt die Mühe. Und nur so lernen Sie etwas dazu.\n",
"\n",
".\n",
@@ -995,7 +1035,7 @@
"2. Wie können Sie diese Anzahl berechnen? Welche Werte benötigen Sie dafür?\n",
"3. Das alles können Sie jetzt schon in Ihre Funktion packen.\n",
"4. Funktioniert das was Sie geschrieben haben auch für andere Werte als 'monty', insbesondere für den Parameter `s` der Funktion?\n",
- "5. Jetzt wo Sie (hoffentlich) ausgerechnet haben, wie viele Leerzeichen Sie benötigen, müssen Sie diese noch erzeugen.\n",
+ "5. Wenn Sie jetzt ausgerechnet haben, wie viele Leerzeichen Sie benötigen, müssen Sie diese noch erzeugen.\n",
"6. Dafür können Sie den Operator `*` für Zeichenkettenwiederholung verwenden. \n",
"7. `' ' * 10` ergibt z.B. 10 Leerzeichen\n",
"8. Jetzt haben Sie genug Leerzeichen ... aber die müssen ja noch vor die Zeichenkette `s`.\n",
@@ -1042,13 +1082,63 @@
"right_justify('Abschlussfrage: was passiert, wenn Sie die Funktion mit einer Zeichenkette aufrufen, die länger als 70 Zeichen ist?')"
]
},
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "#### Aufgabe 1+\n",
+ "Testen Sie folgendermaßen, ob Sie verstanden haben, wie die Funktion `right_justify` funktioniert: Schreiben Sie eine Funktion `center`, die eine als Argument übergebene Zeichenkette zentriert ausgibt (bei einer angenommen maximalen Spaltenbreite von 70, wie gerade eben):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Tipp zur Lösung: Mit dem Operator `//` können wir zwei ganze Zahlen so teilen, dass eine ganze Zahl (*integer*) herauskommt. Während `7 / 2` die Fließkommazahl `3.5` ergibt, erhalten wir bei `7 // 2` die ganze Zahl `3` (es wird stets abgerundet).\n",
+ "\n",
+ "Ein Aufruf der Funktion mit den folgenden Argumenten:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "center('Diese Wörter')\n",
+ "center('stehen')\n",
+ "center('in')\n",
+ "center('der Mitte')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "sollte folgendes Ergebnis liefern:\n",
+ "\n",
+ "```\n",
+ " Diese Wörter\n",
+ " stehen\n",
+ " in\n",
+ " der Mitte\n",
+ "```"
+ ]
+ },
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Aufgabe 2\n",
"\n",
- "Ein Funktionsobjekt ist ein Wert, den wir einer Variable zuweisen können oder auch einer Funktion als Argument übergeben können. Zum Beispiel ist `do_twice` eine funktion, die ein Funktionsobjekt als Argument erwartet und die Funktion dann zweimal aufruft:"
+ "Ein Funktionsobjekt ist ein Wert, den wir einer Variablen zuweisen können oder auch einer Funktion als Argument übergeben können. Zum Beispiel ist `do_twice` eine Funktion, die ein Funktionsobjekt als Argument erwartet und die Funktion dann zweimal aufruft:"
]
},
{
@@ -1080,17 +1170,17 @@
"cell_type": "markdown",
"metadata": {},
"source": [
- "(Tipp vorab: Mit der Tastenkombination `SHIFT STRG -` können Sie so eine Box hier teilen - also `SHIFT` und `STRG` gleichzeitig gedrückt halten und dann die Minustaste drücken. So können Sie die Ihren Code direkt hinter jeder der folgenden Teilaufgaben einfügen.) "
+ "(Tipp: Mit der Tastenkombination `SHIFT STRG -` können wir einen Block teilen - also `SHIFT` und `STRG` gleichzeitig gedrückt halten und dann die Minustaste drücken. So können Sie Ihren Code direkt hinter jeder der folgenden Teilaufgaben einfügen.) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
- "1. Geben Sie dieses Beispiel in eine Code-Box ein und testen Sie es.\n",
+ "1. Geben Sie dieses Beispiel in einen Code-Block ein und testen Sie es.\n",
"2. Ändern Sie `do_twice`, so dass \n",
" - es zwei Argumente erwartet: ein Funktionsobjekt und einen Wert und\n",
- " - die übergebene funktion zweimal aufruft und ihr den Wert als Argument übergibt.\n",
+ " - die übergebene Funktion zweimal aufruft und ihr den Wert als Argument übergibt.\n",
"3. Rufen Sie mit der geänderten Funktion `do_twice` die Funktion `print_twice` (die wir weiter vorne definiert hatten) auf und übergeben Sie ein Wort Ihrer Wahl als Argument.\n",
"4. Definieren Sie eine Funktion `do_four`, die ein Funktionsobjekt und einen Wert erwartet und die übergebene Funktion viermal aufruft und ihr dabei den Wert als Parameter übergibt. Die Funktion `do_four` sollte dabei aus nur zwei Zeilen im Rumpf bestehen, nicht aus vier!\n",
"\n",
@@ -1116,7 +1206,185 @@
"source": [
"#### Bonusaufgabe\n",
"\n",
- "aus der Vorbereitung zur Vorlesung"
+ "Erinnern Sie sich noch an die folgende Aufgabe?\n",
+ "\n",
+ "1. Finden Sie einen Algorithmus zur Lösung des folgenden Problems:\n",
+ " *Gegeben sei eine positive ganze Zahl `n`. Finden Sie eine Liste\n",
+ " von positiven ganzen Zahlen, so dass das Produkt der Zahlen am\n",
+ " größten unter allen positiven ganzen Zahlen ist, deren Summe\n",
+ " gleich `n` ist.*\n",
+ "\n",
+ " Zum Beispiel: \n",
+ " - Für `n = 4` ist die gesuchte Liste `(2,2)`, denn `2 * 2` ist größer als `1 * 1 * 1 * 1`, `2 * 1 * 1` und `3 * 1`.\n",
+ " - Für `n = 5` ist die gesuchte Liste `(2,3)`.\n",
+ "\n",
+ "2. Wie lautet die Liste für `n = 2001`?\n",
+ "3. Erklären Sie, wie Sie \"einen Fuß in die Tür bekommen\" haben.\n",
+ "\n",
+ "Versuchen Sie es zunächst ohne Hilfe. Wie kann Ihnen Python dabei helfen? \n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ "Mein \"Fuß in der Tür\" war, dass ich von Hand eine Tabelle mit den Ergebnissen für die ersten `n` Zahlen gebaut habe:\n",
+ "\n",
+ "| n | Liste | Produkt |\n",
+ "|----|-----------|---------|\n",
+ "| 2 | 1 1 | 1 | \n",
+ "| 3 | 1 2 | 3 | \n",
+ "| 4 | 2 2 | 4 |\n",
+ "| 5 | 2 3 | 6 |"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Ergänzen Sie diese Tabelle von Hand. Dabei kann Ihnen eine Funktion helfen, die für eine gegebene Liste an Zahlen das Produkt und die Summe berechnet:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def prodsum(zahlen):\n",
+ " prod = 1\n",
+ " summ = 0\n",
+ " for zahl in zahlen:\n",
+ " prod = prod * zahl\n",
+ " summ = summ + zahl\n",
+ " print(\"Produkt =\", prod, \"Summe =\", summ)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Eine Liste von Zahlen können wir mit erzeugen, indem wir die Zahlen durch Komma getrennt zwischen zwei Klammern schreiben:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "(2,3)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Wir können also `prodsum` so aufrufen:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "prodsum((2,3))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Testen Sie für jedes `n` mehrere Listen, bis Sie sich jeweils sicher sind, die mit dem größten Produkt gefunden zu haben.\n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ "Ich habe mit Hilfe der Funktion die Tabelle bis `n=15` ergänzt bis ich mir sicher war, dass ich das Prinzip verstanden hatte. \n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ ".\n",
+ "\n",
+ "Sehen Sie jetzt ein Muster in der Tabelle? Die Produkte bestehen nur aus 3en und ggf. noch 2en oder 4en. Genauer:\n",
+ "\n",
+ "Beobachtung (\"Fuß in der Tür\"): \n",
+ "- Ein Produkt aus möglichst vielen Dreien ergibt das beste Ergebnis.\n",
+ "- Falls es nicht ganz aufgeht, mit 2 oder 4 auffüllen.\n",
+ "\n",
+ "Erklärung (warum Dreien?):\n",
+ "- Ob wir eine Vier oder zwei Zweien nehmen, ist egal, da `2+2 = 4 = 2*2`.\n",
+ "- Da `2+3=5` aber `2*3=6`, lohnt es sich nicht, größere Zahlen zu nehmen\n",
+ " (ebenso: `3+3=6` aber `3*3=9`) - das Produkt der kleinen Zahlen ist stets größer als ihre Summe\n",
+ "\n",
+ "Algorithmus:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def produkt_summe(n):\n",
+ " \"\"\"Berechnet für gegebenes n>2 das Produkt derjenigen Liste von\n",
+ " Zahlen, deren Summe n ergibt und gleichzeitig die größte Liste mit\n",
+ " dieser Eigenschaft ist.\n",
+ " \n",
+ " Vorgehen: wiederholt 3 von n abziehen, bis der Rest kleiner oder \n",
+ " gleich 4 ist. (letzter Schritt klappt, weil 2+2=4=2*2)\n",
+ "\n",
+ " \"\"\"\n",
+ " rest = n\n",
+ " prod = 1\n",
+ " zahlen = []\n",
+ " while rest > 4:\n",
+ " rest = rest - 3\n",
+ " prod = prod * 3\n",
+ " zahlen.append(3)\n",
+ " prod = prod * rest\n",
+ " zahlen.append(rest)\n",
+ " \n",
+ " print(\"*\".join([str(z) for z in zahlen]), \"=\", prod)\n",
+ " print(\"+\".join([str(z) for z in zahlen]), \"=\", sum(zahlen))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Testen wir es einmal aus:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "produkt_summe(14)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "Das sollte auch die Zahl sein, die Sie für `n=14` oben in Ihrer Tabelle stehen haben. \n",
+ "\n",
+ "Die Funktion verwendet zwar ein paar Dinge, um eine schöne Ausgabe zu erzeugen, aber die wesentliche Funktionalität in der `while`-Schleife zur Berechnung des Produkts besteht nur aus Konstrukten, die wir schon kennengelernt haben. \n",
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "([PythoRandall Munroe\n",
+ "\n"
]
},
{
--
GitLab