Newer
Older
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def polyline(t, n, length, angle):\n",
" \"\"\"Draws n line segments with the given length and\n",
" angle (in degrees) between them. t is a turtle.\n",
" \"\"\" \n",
" for i in range(n):\n",
" t.fd(length)\n",
" t.lt(angle)\n",
" \n",
" \n",
"\n",
"#turtle.mainloop()\n",
"#turtle.bye()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Es gilt die Konvention, dass Docstrings in dreifachen Anführungszeichen gesetzt werden. Mit Hilfe der dreifachen Anführungszeichen kann der Text über mehr als eine Zeile hinwegreichen.\n",
"\n",
"Der Docstring im Beispiel ist knapp, enthält aber die wesentlichen Informationen, die jemand benötigt, der die Funktion nutzen möchte. Es wird prägnant erklärt, was die Funktion tut (ohne groß zu beschreiben, wie sie es tut). Es wird auch erklärt, welche Auswirkung jeder Parameter auf das Verhalten der Funktion hat und von welchem Typ jeder Parameter sein sollte (falls es nicht offensichtlich ist). \n",
"\n",
"Das Schreiben dieser Art von Dokumentation ist ein wichtiger Teil des Schnittstellenentwurfs. Eine gut konzipierte Schnittstelle sollte einfach zu erklären sein. Falls es Ihnen schwerfällt, Ihre Funktionen zu erklären, dann könnte es vielleicht helfen, die Schnittstelle zu verbessern. \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Eine Schnittstelle ist wie ein Vertrag zwischen der Funktion und den Aufrufenden. Die Aufrufenden stimmen zu, bestimmte Parameter bereitzustellen und die Funktion stimmt zu, eine bestimmte Aufgabe zu erledigen.\n",
"\n",
"Beispielsweise benötigt die Funktion `polyline` vier Parameter:\n",
"- `t` muss eine Schildkröte (Typ `Turtle`) sein,\n",
"- `n` muss eine ganze Zahl sein,\n",
"- `length` muss eine positive Zahl sein,\n",
"- `angle` muss eine Zahl sein, die einen Winkel in Grad darstellt.\n",
"\n",
"Diese Anforderungen nennen wir auch **Vorbedingungen**, denn es wird vorausgesetzt, dass sie erfüllt sind, bevor die Funktion ausgeführt wird. Umgekehrt heißen Bedingungen am Ende einer Funktion **Nachbedingungen**. Nachbedingungen schließen die beabsichtigte Wirkung der Funktion (wie z.B. ein Linienstück zeichnen) und etwaige Nebeneffekte (wie z.B. die Schildkröte zu bewegen oder andere Änderungen vorzunehmen) ein. \n",
"\n",
"Die Erfüllung der Vorbedingungen ist die Aufgabe der Aufrufenden. Wenn die Aufrufenden eine (ordentlich dokumentierte!) Vorbedingung verletzen und die Funktion arbeitet nicht richtig, dann liegt der Fehler bei den Aufrufenden, nicht bei der Funktion.\n",
"\n",
"Wenn die Vorbedingungen erfüllt sind und die Nachbedingungen sind es nicht, dann liegt der Fehler bei der Funktion. Wenn ihre Vor- und Nachbedingungen klar und deutlich sind, dann kann das sehr beim Debugging helfen.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Legen wir uns eine Liste mit den wichtigsten Begriffen an, die wir im Kapitel 4 gelernt haben:\n",
"\n",
"- Methode:\n",
"- Schleife: Eine Schleife ist eine Folge von Anweisungen, die mehrfach hintereinander ausgeführt werden.\n",
"- Verkapselung: \n",
"- Verallgemeinerung:\n",
"- Schlüsselwortargument:\n",
"- Schnittstelle:\n",
"- Entwicklungsplan:\n",
"- Docstring:\n",
"- Vorbedingung:\n",
"- Nachbedingung:\n",
"\n",
"Ergänzen Sie die Liste in eigenen Worten. Das ist eine gute Erinnerungs- und Übungsmöglichkeit."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Laden Sie den gesamten Code für dieses Kapitel [hier](http://thinkpython2.com/code/polygon.py) herunter. Dieser Code ist weitestgehend deckungsgleich mit dem Code, den wir in diesem Kapitel angesehen haben, kann aber sehr hilfreich sein, wenn Sie nicht in Jupyter Notebooks arbeiten können. \n",
"Um Probleme mit Turtle+Jupyter zu vermeiden, stellen Sie sicher, dass am Ende Ihres Programmes stets die folgenden beiden Zeilen stehen:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"turtle.mainloop()\n",
"turtle.bye()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. Zeichnen Sie (mit Stift und Papier) ein Stapeldiagramm (siehe [Kapitel 3](#3.9-Stapel-Diagramme)), welches den Zustand des Programms zeigt, während die Anweisung `circle(bob, radius)` ausgeführt wid. Sie können das manuell herausfinden oder `print`-Anweisungen zum Code hinzufügen. (*Hinweis: Unter Umständen kann Ihnen [Python-Tutor](http://pythontutor.com/) dabei helfen*)\n",
"2. Die Version der Funktion `arc` in [Abschnitt 4.7](#4.7-Refactoring) ist nicht besonders präzise, denn die lineare Näherung eines Kreises ist immer ausserhalb des wahren Kreises. Daher steht die Schildkröte am Ende immer ein paar Pixel vom richtigen Ziel entfernt. Die Lösung im Python-Code zeigt eine Möglichkeit, die Auswirkung dieses Fehlers zu reduzieren. Lesen Sie sich den Code durch und schauen Sie, ob das für Sie einen Sinn ergibt. Vielleicht hilft es Ihnen weiter, ein Diagramm zu zeichnen."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"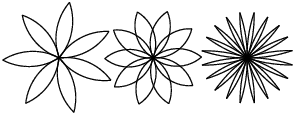\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Blumen.\n",
"\n",
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
1139
1140
1141
1142
1143
1144
1145
1146
1147
1148
1149
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1165
1166
1167
1168
1169
1170
1171
1172
1173
1174
1175
1176
1177
1178
1179
1180
1181
1182
1183
1184
1185
1186
1187
1188
1189
1190
1191
1192
1193
1194
1195
1196
1197
1198
1199
1200
1201
1202
1203
1204
1205
1206
1207
1208
1209
1210
1211
1212
1213
1214
1215
1216
1217
1218
1219
1220
1221
1222
1223
1224
1225
1226
1227
1228
1229
1230
1231
1232
1233
1234
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-info\">Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Die Lösung benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py). \n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Wenn Sie sich die Blume ansehen, können Sie feststellen, dass zwei Teile ineinander greifen um die Blume zu erzeugen. Welche Teile sind das?\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Die Blütenblätter werden einzeln hintereinander gezeichnet, konzentrieren Sie sich also zuerst darauf, ein einzelnes Blütenblatt zu zeichnen.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Überlegen Sie wie der Kopf der Blütenblattfunktion aussehen muss und schreiben Sie diese. \n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Sie müssen der Funktion eine Schildkröte übergeben, die das Blatt zeichnen soll. Die Funktion braucht auch den Radius des Kreisbogens, welcher die Länge des Blatts bestimmt und den Winkel in dem das Blatt gezeichnet werden soll und damit wie breit des Blütenblatt wird.\n",
"\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Wie im vorherigen Hinweis schon angesprochen besteht das Blütenblatt aus 2 Kreisbögen. Verwenden Sie eine Schleife und `arc` um das Blatt zu zeichnen. Vergessen Sie nicht, die Funktion zu testen. \n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Nach dem ersten Kreisbogen muss die Schildkröte sich soweit drehen, dass sie mit dem nächsten Kreisbogen eine volle 180° Drehung vollzogen hat.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Wenn Sie ein einzelnes Blütenblatt zeichnen können gilt es nun sich zu überlegen, wie man die Blütenblätter zu einer Blume zusammenfügen kann. Schreiben Sie den Kopf der Blumen Funktion und überlegen Sie, welche Informationen der Funktion übergeben werden müssen\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Da die Blumenfunktion Informationen an die Blütenblatt Funktion weitergeben muss, muss die Funktion die selben Parameter erhalten. Zusätzlich muss die Funktion noch gesagt bekommen, wie viele Blütenblätter gezeichnet werden sollen.\n",
" \n",
" </div> \n",
"</details>\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Um die richtige Anzahl an Blütenblättern zu zeichnen müssen Sie die Funktion \"Blatt\" innerhalb der Funktion \"Blume\" entsprechend oft aufrufen, verwenden Sie dafür eine Schleife.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Um die Blütenblätter gleichmäßig um den Mittelpunkt der Blume zu verteilen, muss der Winkel zwischen den Blättern so berechnet werden, dass nach Vollenden der Blume eine 360° Wendung vollzogen wurde. Überlegen Sie wie Sie dabei vorgehen müssen?\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">11. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Dafür muss der Winkel zwischen den Blättern 360/n betragen, wobei n für die Anzahl der Blätter steht.\n",
"\n",
" </div> \n",
"</details>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
"\n",
"(Quelle: Jason Eppink, Flickr)\n",
"Hier ist eine weitere mögliche [Lösung](http://thinkpython2.com/code/flower.py)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import math\n",
"import turtle\n",
"bob=turtle.Turtle()\n",
"\n",
"# Damit diese Lösung funktioniert müssen die Funktionen arc und polyline schon definiert worden sein.\n",
"\n",
"def blatt(t, r, angle):\n",
" for i in range (2):\n",
" arc(t,r, angle)\n",
" t.lt(180.0-angle)\n",
" \n",
" \n",
"def blume(t,r,angle,n):\n",
" for i in range (n):\n",
" blatt (t,r,angle)\n",
" t.lt(360/n)\n",
"\n",
"blume(bob,60.0,60.0,5)\n",
"\n",
"turtle.mainloop() \n",
"turtle.bye()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Figuren.\n",
1296
1297
1298
1299
1300
1301
1302
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1314
1315
1316
1317
1318
1319
1320
1321
1322
1323
1324
1325
1326
1327
1328
1329
1330
1331
1332
1333
1334
1335
1336
1337
1338
1339
1340
1341
1342
1343
1344
1345
1346
1347
1348
1349
1350
1351
1352
1353
1354
1355
1356
1357
1358
1359
1360
1361
1362
1363
1364
1365
1366
1367
1368
1369
1370
1371
1372
1373
1374
1375
1376
1377
1378
1379
1380
1381
1382
1383
1384
1385
1386
1387
1388
1389
1390
1391
1392
1393
1394
"\n",
"\n",
"Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Wir gehen analog zu Blume vor, und zeichnen die einzelnen \"Kuchenstücke\" bevor wir sie zu dem \"Kuchen\" zusammensetzen.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Erzeugen Sie zunächst den Kopf der Funktion für ein einzelnes Kuchenstück. Überlegen Sie anschließend, wie Sie das Dreieck zeichnen könnten. Welche Informationen müssen dem Kopf der Funktion übergeben werden?\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Die Funktion für das Kuchenstück muss die Schildkröte, die Seitenlänge (die der Radius der Form \"Kuchen ist, daher nennen wir sie \"r\") und den Winkel übergeben bekommen, in dem das Kuchenstück gezeichnet werden soll. \n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Da wir die beiden Seitenlängen vorgeben, müssen wir die obere Länge in Abhängigkeit von den Seitenlängen (dem Radius der Form Kuchen und dem Winkel berechnen. Wir verwenden das sogenannte Bogenmaß. Die vollständige dafür Formel ist $2*r*sin(angle*\\pi/180)$ \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Um Herauszufinden, wie weit sich die Schildkröte drehen muss, ist es am Einfachsten verschiedene Drehwinkel auszuprobieren, bis es funktioniert. Verwenden Sie 90 Winkel als Basis und addieren oder subtrahieren Sie den Winkel aus dem Funktionskopf\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Damit die Schildkröte den gesamten Kuchen zeichnen kann muss Sie immer in derselben Position starten und enden. Dafür muss Sie sich zu Beginn im angegebenen Winkel drehen und am Ende soweit, dass sie wieder die Ausgangsposition annimmt. Um die Position wieder anzunehmen muss sich die Schildkröte um weniger als 180 Grad drehen. Der genaue Winkel kann mit Hilfe des Winkel-Parameters berechnet werden. \n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Um die Kuchen-Funktion zu schreiben können Sie die Blume-Funktion kopieren und anpassen. Es müssen einige Veränderungen vorgenommen werden. Überlegen Sie welche Änderungen das sind. Um einen Eindruck zu bekommen, können Sie Kuchen aufrufen und sehen welche Fehler auftreten.\n",
"\n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Damit der Kuchen ohne Lücken gezeichnet werden kann muss der Winkel berechnet werden und nicht der Funktion übergeben werden. Im Funktionskopf muss also nur der Radius der Figur, also die Seitenlänge der einzelnen Stücke, die Schildkröte und die Anzahl der Stücke übergeben werden. Der Winkel wird dann in Abhängigkeit von der Anzahl der Stücke berechnet.\n",
"\n",
" \n",
" </div> \n",
"</details>\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
"\n",
"Der Winkel zwischen den Stücken ist, da wir eine volle Drehung vornehmen wollen 360 geteilt durch die Anzahl der Stücke. In der Schleife rufen wir Stück auf, dort müssen wir den Winkel anpassen, bevor wir die entsprechende Drehung vornehmen. Führen Sie die Funktion aus und versuchen Sie herauszufinden, wie Sie den Winkel in stück anpassen müssen.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Der Winkel für Stück ist der halbe Winkel zwischen Stücken. Wir nehmen also die Winkelvariable/2 als zu übergebenden Wert.\n",
"\n",
" </div> \n",
"</details>\n"
1395
1396
1397
1398
1399
1400
1401
1402
1403
1404
1405
1406
1407
1408
1409
1410
1411
1412
1413
1414
1415
1416
1417
1418
1419
1420
1421
1422
1423
1424
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
"\n",
"(Quelle: Jason Eppink, Flickr)\n",
"\n",
"*(Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/pie.py))*"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import math\n",
"import turtle\n",
"\n",
"# Arbeiten Sie diese Lösung durch und kommentieren Sie die einzelnen Schritte\n",
"\n",
1427
1428
1429
1430
1431
1432
1433
1434
1435
1436
1437
1438
1439
1440
1441
1442
1443
1444
1445
1446
1447
"def stück (t,r, angle):\n",
" c=2*r*(math.sin(angle*math.pi/180))\n",
" t.rt(angle)\n",
" t.fd(r)\n",
" t.lt(90+angle)\n",
" t.fd(c)\n",
" t.lt(90+angle)\n",
" t.fd(r)\n",
" t.lt(180-angle)\n",
"\n",
"\n",
"def kuchen (t, n, r):\n",
" angle=360/n\n",
" for i in range (n):\n",
" stück(t,r,angle/2)\n",
" t.lt(angle)\n",
" turtle.mainloop()\n",
" turtle.bye()\n",
" \n",
" \n",
"bob=turtle.Turtle() \n",
"kuchen(bob, 5, 100)\n",
"\n",
"turtle.mainloop() \n",
"turtle.bye()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
1458
1459
1460
1461
1462
1463
1464
1465
1466
1467
1468
1469
1470
1471
1472
1473
1474
1475
1476
1477
1478
1479
1480
1481
1482
1483
1484
1485
1486
1487
1488
1489
1490
1491
1492
1493
1494
1495
1496
1497
1498
1499
1500
1501
1502
1503
1504
1505
1506
1507
1508
1509
1510
1511
1512
1513
1514
1515
1516
1517
1518
"### Aufgabe 4\n",
"\n",
"\n",
"Lesen Sie etwas zu Spiralen auf [Wikipedia](https://de.wikipedia.org/wiki/Spirale). Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"In dieser Aufgabe, können Sie entscheiden, wie komplex Sie die Schnittstelle gestalten wollen. Sie müssen mindestens die Schildkröte übergeben, die die Spirale zeichnen soll, in maximaler Komplexität kann der Nutzer alle Variablen der Spirale anpassen. Hier wurde entschieden, dass der Nutzer lediglich die Schildkröte und die Anzahl der Spiralensegmente angeben darf, wenn Sie eine komplexere Lösung haben wollen, fügen Sie diese Parameter dem Funktionsaufruf hinzu.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Die Formel für die Berechnung von Spiralen ist $r = a + b*\\theta$. Dabei können Sie einfach Ausgangswerte für a und b festlegen. Ein geeigneter Wert für a ist zum Beispiel 0.1 und für b 0.0002. Wenn ihre Funktion funktioniert, probieren Sie verschiedene Werte für a und b aus und sehen Sie sich an, wie die Spirale sich verändert. \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Weitere Parameter können entweder in der Schnittstelle oder aber wie in dem Beispiel unten in der Funktion festgelegt werden. Diese Parameter sind der Ausgangswinkel theta der Spirale und die Länge der einzelnen Spiralensegmente.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Analog zum Kreisbogen wird auch die Spirale durch kurze gerade Segmente und Drehungen gezeichnet. Da das Zeichnen von Segmenten n-mal wiederholt wird, benötigen Sie eine for-Schleife.\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"In der Schleife muss für jedes Segment neu berechnet werden wie weit die Schildkröte sich drehen muss, da der Winkel nicht konstant bleibt. Dafür verwendet die Lösung: dtheta = 1 / (a + b * theta)\n",
" \n",
" </div> \n",
"</details>\n",
"\n",
"\n",
"<details>\n",
" <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
" <div class=\"alert alert-info\" role=\"alert\">\n",
" \n",
"Da diese Formel theta als den Winkel des vorherigen Abschnitts verwendet, muss theta ebenfalls in jedem Schleifendurchlauf überschrieben werden - also addieren Sie dtheta auf theta auf. \n",
" \n",
" </div> \n",
"</details>\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a data-flickr-embed=\"true\" href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
"\n",
1535
1536
1537
1538
1539
1540
1541
1542
1543
1544
1545
1546
1547
1548
1549
1550
1551
1552
1553
1554
1555
1556
1557
1558
1559
1560
1561
1562
1563
1564
1565
1566
1567
1568
"Eine [Lösung](http://thinkpython2.com/code/spiral.py)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def spirale(t,n):\n",
" '''In dieser Spirale bestimmt der Nutzer, wie viele Segmente gezeichnet werden, die Windung der Spirale ist\n",
" in der Funktion festgelegt.\n",
" '''\n",
" length=3 \n",
" a=0.1\n",
" b=0.0002\n",
" theta=0.0\n",
" for i in range (n):\n",
" t.fd(length)\n",
" dtheta = 1 / (a + b * theta)\n",
" t.lt(dtheta)\n",
" theta = theta + dtheta\n",
"\n",
"import turtle\n",
"bob=turtle.Turtle() \n",
"spirale(bob,1000)\n",
"turtle.mainloop()\n",
"turtle.bye()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*(Hinweis: Dies ist eher eine Fleiß- und Zusatzaufgabe.)*\n",
"\n",
"Die Buchstaben des Alphabets sind aus ein paar grundlegenden Elementen zusammengesetzt wie z.B. vertikalen und horizontalen Linien und einigen Kurven. Entwerfen Sie ein Alphabet, welches mit einer kleinen Anzahl einfacher Elemente gezeichnet werden kann und schreiben Sie dann Funktionen zum Zeichnen der Buchstaben. \n",
"\n",
"Sie sollten eine Funktion für jeden Buchstaben schreiben, die Sie `draw_a`, `draw_b`, etc. nennen und diese Funktionen in eine Datei namens `letters.py` packen. Sie können [hier](http://thinkpython2.com/code/typewriter.py) eine \"Schildkrötenschreibmaschine\" herunterladen und damit ihren Code testen.\n",
"\n",
"\n",
"Das könnte dann so aussehen:\n",
"\n",
"Sie finden eine Lösung für diese Aufgabe [hier](http://thinkpython2.com/code/letters.py); Diese benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py)."
{
"cell_type": "markdown",
"metadata": {},
"source": [
" Speichern Sie dieses Notebook, so dass Ihre Änderungen nicht verlorengehen (nicht auf einem Pool-Rechner). Klicken Sie dazu oben links auf das Disketten-Icon und nutzen Sie beispielsweise einen USB-Stick, E-Mail, Google Drive, Dropbox oder Ihre [HU-Box](https://box.hu-berlin.de/). "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"Herzlichen Glückwunsch! Sie haben das 4. Kapitel geschafft. Weiter geht es in [5: Bedingungen und Rekursion](seminar05.ipynb)."