seminar04.ipynb

  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import turtle \n",
    "\n",
    "bob = turtle.Turtle()\n",
    "\n",
    "polyline(bob, 8, 30, 30)\n",
    "\n",
    "turtle.mainloop()\n",
    "turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Jetzt können wir die Funktionen `polygon` und `arc` umschreiben, sodass sie die Funktion `polyline` nutzen:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import turtle\n",
    "\n",
    "def polyline(t, n, length, angle):\n",
    "    '''zeichnet einen Teil eines Vielecks in Abhängigkeit von der Anzahl der Ecken n, der Länge length \n",
    "    und der Drehung an jeder Ecke (angle)'''\n",
    "    for i in range(n):\n",
    "        t.fd(length)\n",
    "        t.lt(angle)\n",
    "        \n",
    "def arc(t, r, angle):\n",
    "    '''zeichnet einen Kreisbogen in Abhängigkeit von Radius r und Winkel angle'''\n",
    "    arc_length = 2 * math.pi * r * angle / 360\n",
    "    n = int(arc_length / 3) + 1\n",
    "    step_length = arc_length / n\n",
    "    step_angle = float(angle) / n\n",
    "    polyline(t, n, step_length, step_angle)\n",
    "    \n",
    "\n",
    "#turtle.mainloop()\n",
    "#turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Und schließlich können wir die Funktion `circle` umschreiben, sodass sie die Funktion `arc` nutzt:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import turtle\n",
    "\n",
    "def polyline(t, n, length, angle):\n",
    "    '''zeichnet einen Teil eines Vielecks in Abhängigkeit von der Anzahl der Ecken n, der Länge length \n",
    "    und der Drehung an jeder Ecke (angle)'''\n",
    "    for i in range(n):\n",
    "        t.fd(length)\n",
    "        t.lt(angle)\n",
    "        \n",
    "def arc(t, r, angle):\n",
    "    '''zeichnet einen Kreisbogen in Abhängigkeit von Radius r und Winkel angle'''\n",
    "    arc_length = 2 * math.pi * r * angle / 360\n",
    "    n = int(arc_length / 3) + 1\n",
    "    step_length = arc_length / n\n",
    "    step_angle = float(angle) / n\n",
    "    polyline(t, n, step_length, step_angle)\n",
    "    \n",
    "def circle(t, r):\n",
    "    '''zeichnet einen Kreis mit Radius r'''\n",
    "    arc(t, r, 360)\n",
    "    \n",
    "    \n",
    "    \n",
    "#turtle.mainloop()\n",
    "#turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Dieser Prozess der Umstrukturierung eines Programms und der Verbesserung von Schnittstellen nennt sich **Refactoring** und hilft Code wiederverwenden zu können. In unserem Fall haben wir festgestellt, dass `arc` und `polygon` ähnlichen Code enthalten haben, daher haben wir diesen Code umgestaltet und in die Funktion `polyline` \"ausfaktorisiert\", also quasi ausgeklammert.\n",
    "\n",
    "Hätten wir vorausschauend geplant, hätten wir vielleicht `polyline` zuerst geschrieben und diese Umstrukturierung vermieden. Oft wissen wir aber am Anfang eines Projektes noch nicht genug, um schon alle Schnittstellen entwerfen zu können. Sobald wir anfangen zu programmieren, verstehen wir das Problem besser. Manchmal ist Refactoring ein Anzeichen dafür, dass wir etwas gelernt haben.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Ein Entwicklungsplan\n",
    "\n",
    "Ein **Entwicklungsplan** ist ein Prozess zum Schreiben von Programmen. Der Prozess, den wir in dieser Fallstudie verwendet haben, heißt \"Verkapselung und Verallgemeinerung\". Die Schritte dieses Prozesses sind:\n",
    "\n",
    "1. Wir schreiben ein kleines Programm ohne Funktionsdefinitionen.\n",
    "2. Sobald das Programm funktioniert, identifizieren wir ein schlüssiges und zusammengehöriges Stück Code, verkapseln es in einer Funktion und geben ihm einen Namen.\n",
    "3. Wir verallgemeinern die Funktion durch Hinzufügen geeigneter Parameter.\n",
    "4. Wir wiederholen die Schritte 1 bis 3 bis wir eine Menge funktionierender Funktionen haben. Dabei kopieren wir Code und fügen ihn an der richtigen Stelle ein, um nochmaliges Eintippen zu vermeiden (und das damit ggf. verbundene Debugging).\n",
    "5. Wir suchen nach Möglichkeiten, das Programm durch Refactoring zu verbessern. Wenn wir beispielsweise ähnlichen Code an verschiedenen Stellen haben, können wir überlegen, ob wir ihn nicht besser in eine geeignete allgemeine Funktion ausklammern. \n",
    "\n",
    "\n",
    "Dieser Prozess hat einige Nachteile (wir schauen uns Alternativen später an), aber er ist praktisch, wenn wir vorab nicht wissen, wie wir das Programm in Funktionen aufteilen könnten. Dieser Ansatz ermöglicht uns den Entwurf des Programms während wir es schreiben.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Docstring\n",
    "\n",
    "Ein **Docstring** ist eine Zeichenkette am Anfang einer Funktion, die die Schnittstelle der Funktion erklärt (\"doc\" ist kurz für \"documentation\", also Dokumentation). Hier ist ein Beispiel:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import turtle\n",
    "\n",
    "def polyline(t, n, length, angle):\n",
    "    \"\"\"Draws n line segments with the given length and\n",
    "    angle (in degrees) between them.  t is a turtle.\n",
    "    \"\"\"    \n",
    "    for i in range(n):\n",
    "        t.fd(length)\n",
    "        t.lt(angle)\n",
    "       \n",
    "    \n",
    "\n",
    "#turtle.mainloop()\n",
    "#turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Es gilt die Konvention, dass Docstrings in dreifachen Anführungszeichen gesetzt werden. Mit Hilfe der dreifachen Anführungszeichen kann der Text über mehr als eine Zeile hinwegreichen.\n",
    "\n",
    "Der Docstring im Beispiel ist knapp, enthält aber die wesentlichen Informationen, die jemand benötigt, der die Funktion nutzen möchte. Es wird prägnant erklärt, was die Funktion tut (ohne groß zu beschreiben, wie sie es tut). Es wird auch erklärt, welche Auswirkung jeder Parameter auf das Verhalten der Funktion hat und von welchem Typ jeder Parameter sein sollte (falls es nicht offensichtlich ist). \n",
    "\n",
    "Das Schreiben dieser Art von Dokumentation ist ein wichtiger Teil des Schnittstellenentwurfs. Eine gut konzipierte Schnittstelle sollte einfach zu erklären sein. Falls es Ihnen schwerfällt, Ihre Funktionen zu erklären, dann könnte es vielleicht helfen, die Schnittstelle zu verbessern. \n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "##  Debugging\n",
    "\n",
    "Eine Schnittstelle ist wie ein Vertrag zwischen der Funktion und den Aufrufenden. Die Aufrufenden stimmen zu, bestimmte Parameter bereitzustellen und die Funktion stimmt zu, eine bestimmte Aufgabe zu erledigen.\n",
    "\n",
    "Beispielsweise benötigt die Funktion `polyline` vier Parameter:\n",
    "- `t` muss eine Schildkröte (Typ `Turtle`) sein,\n",
    "- `n` muss eine ganze Zahl sein,\n",
    "- `length` muss eine positive Zahl sein,\n",
    "- `angle` muss eine Zahl sein, die einen Winkel in Grad darstellt.\n",
    "\n",
    "Diese Anforderungen nennen wir auch **Vorbedingungen**, denn es wird vorausgesetzt, dass sie erfüllt sind, bevor die Funktion ausgeführt wird. Umgekehrt heißen Bedingungen am Ende einer Funktion **Nachbedingungen**. Nachbedingungen schließen die beabsichtigte Wirkung der Funktion (wie z.B. ein Linienstück zeichnen) und etwaige Nebeneffekte (wie z.B. die Schildkröte zu bewegen oder andere Änderungen vorzunehmen) ein.  \n",
    "\n",
    "Die Erfüllung der Vorbedingungen ist die Aufgabe der Aufrufenden. Wenn die Aufrufenden eine (ordentlich dokumentierte!) Vorbedingung verletzen und die Funktion arbeitet nicht richtig, dann liegt der Fehler bei den Aufrufenden, nicht bei der Funktion.\n",
    "\n",
    "Wenn die Vorbedingungen erfüllt sind und die Nachbedingungen sind es nicht, dann liegt der Fehler bei der Funktion. Wenn ihre Vor- und Nachbedingungen klar und deutlich sind, dann kann das sehr beim Debugging helfen.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "##  Glossar\n",
    "\n",
    "Legen wir uns eine Liste mit den wichtigsten Begriffen an, die wir im Kapitel 4 gelernt haben:\n",
    "\n",
    "- Methode:\n",
    "- Schleife: Eine Schleife ist eine Folge von Anweisungen, die mehrfach hintereinander ausgeführt werden.\n",
    "- Verkapselung: \n",
    "- Verallgemeinerung:\n",
    "- Schlüsselwortargument:\n",
    "- Schnittstelle:\n",
    "- Refactoring: \n",
    "- Entwicklungsplan:\n",
    "- Docstring:\n",
    "- Vorbedingung:\n",
    "- Nachbedingung:\n",
    "\n",
    "Ergänzen Sie die Liste in eigenen Worten. Das ist eine gute Erinnerungs- und Übungsmöglichkeit."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Übung\n",
    "\n",
    "### Aufgabe 1\n",
    "\n",
    "Laden Sie den gesamten Code für dieses Kapitel [hier](http://thinkpython2.com/code/polygon.py) herunter. Dieser Code ist weitestgehend deckungsgleich mit dem Code, den wir in diesem Kapitel angesehen haben, kann aber sehr hilfreich sein, wenn Sie nicht in Jupyter Notebooks arbeiten können. \n",
    "\n",
    "Um Probleme mit Turtle+Jupyter zu vermeiden, stellen Sie sicher, dass am Ende Ihres Programmes stets die folgenden beiden Zeilen stehen:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "turtle.mainloop()\n",
    "turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "1. Zeichnen Sie (mit Stift und Papier) ein Stapeldiagramm (siehe [Kapitel 3](#3.9-Stapel-Diagramme)), welches den Zustand des Programms zeigt, während die Anweisung `circle(bob, radius)` ausgeführt wid. Sie können das manuell herausfinden oder `print`-Anweisungen zum Code hinzufügen. (*Hinweis: Unter Umständen kann Ihnen [Python-Tutor](http://pythontutor.com/) dabei helfen*)\n",
    "2. Die Version der Funktion `arc` in [Abschnitt 4.7](#4.7-Refactoring) ist nicht besonders präzise, denn die lineare Näherung eines Kreises ist immer ausserhalb des wahren Kreises. Daher steht die Schildkröte am Ende immer ein paar Pixel vom richtigen Ziel entfernt. Die Lösung im Python-Code zeigt eine Möglichkeit, die Auswirkung dieses Fehlers zu reduzieren. Lesen Sie sich den Code durch und schauen Sie, ob das für Sie einen Sinn ergibt. Vielleicht hilft es Ihnen weiter, ein Diagramm zu zeichnen."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Aufgabe 2\n",
    "\n",
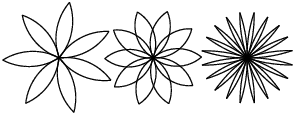    "![Schildkröten-Blumen](http://greenteapress.com/thinkpython2/html/thinkpython2003.png)\n",
    "\n",
    "Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Blumen.\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-info\">Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Die Lösung benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py).      \n",
    "  \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Wenn Sie sich die Blume ansehen, können Sie feststellen, dass zwei Teile ineinander greifen um die Blume zu erzeugen. Welche Teile sind das?\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Die Blütenblätter werden einzeln hintereinander gezeichnet, konzentrieren Sie sich also zuerst darauf, ein einzelnes Blütenblatt zu zeichnen.\n",
    "      \n",
    "   </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Überlegen Sie wie der Kopf der Blütenblattfunktion aussehen muss und schreiben Sie diese. \n",
    "    \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Sie müssen der Funktion eine Schildkröte übergeben, die das Blatt zeichnen soll. Die Funktion braucht auch den Radius des Kreisbogens, welcher die Länge des Blatts bestimmt und den Winkel in dem das Blatt gezeichnet werden soll und damit wie breit des Blütenblatt wird.\n",
    "\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Wie im vorherigen Hinweis schon angesprochen besteht das Blütenblatt aus 2 Kreisbögen. Verwenden Sie eine Schleife und `arc` um das Blatt zu zeichnen. Vergessen Sie nicht, die Funktion zu testen. \n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Nach dem ersten Kreisbogen muss die Schildkröte sich soweit drehen, dass sie mit dem nächsten Kreisbogen eine volle 180° Drehung vollzogen hat.\n",
    "      \n",
    "   </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Wenn Sie ein einzelnes Blütenblatt zeichnen können gilt es nun sich zu überlegen, wie man die Blütenblätter zu einer Blume zusammenfügen kann. Schreiben Sie den Kopf der Blumen Funktion und überlegen Sie, welche Informationen der Funktion übergeben werden müssen\n",
    "     \n",
    " </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Da die Blumenfunktion Informationen an die Blütenblatt Funktion weitergeben muss, muss die Funktion die selben Parameter erhalten. Zusätzlich muss die Funktion noch gesagt bekommen, wie viele Blütenblätter gezeichnet werden sollen.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Um die richtige Anzahl an Blütenblättern zu zeichnen müssen Sie die Funktion \"Blatt\" innerhalb der Funktion \"Blume\" entsprechend oft aufrufen, verwenden Sie dafür eine Schleife.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Um die Blütenblätter gleichmäßig um den Mittelpunkt der Blume zu verteilen, muss der Winkel zwischen den Blättern so berechnet werden, dass nach Vollenden der Blume eine 360° Wendung vollzogen wurde. Überlegen Sie wie Sie dabei vorgehen müssen?\n",
    "      \n",
    "   </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">11. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Dafür muss der Winkel zwischen den Blättern 360/n betragen, wobei n für die Anzahl der Blätter steht.\n",
    "\n",
    "  </div>       \n",
    "</details>"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "\n",
    "\n",
    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
    "\n",
    "(Quelle: Jason Eppink, Flickr)\n",
    "\n",
    "\n",
    "Hier ist eine weitere mögliche [Lösung](http://thinkpython2.com/code/flower.py)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import math\n",
    "import turtle\n",
    "bob=turtle.Turtle()\n",
    "\n",
    "# Damit diese Lösung funktioniert müssen die Funktionen arc und polyline schon definiert worden sein.\n",
    "\n",
    "def blatt(t, r, angle):\n",
    "    for i in range (2):\n",
    "        arc(t,r, angle)\n",
    "        t.lt(180.0-angle)\n",
    "    \n",
    "    \n",
    "def blume(t,r,angle,n):\n",
    "    for i in range (n):\n",
    "        blatt (t,r,angle)\n",
    "        t.lt(360/n)\n",
    "\n",
    "blume(bob,60.0,60.0,5)\n",
    "\n",
    "turtle.mainloop() \n",
    "turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Aufgabe 3\n",
    "\n",
    "![Schildkröten-Kuchen](http://greenteapress.com/thinkpython2/html/thinkpython2004.png)\n",
    "\n",
    "Schreiben Sie eine möglichst allgemeine Menge an Funktionen zum Zeichnen von solchen Figuren.\n",
    "\n",
    "\n",
    "Wie Sie inzwischen vielleicht erwarten folgen jetzt Hinweise dazu, wie Sie die Aufgabe angehen können. Versuchen Sie die Aufgabe in Partnerarbeit zu lösen und verwenden Sie so wenige Hinweise wie möglich, das ist die beste Übung: \n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Wir gehen analog zu Blume vor, und zeichnen die einzelnen \"Kuchenstücke\" bevor wir sie zu dem \"Kuchen\" zusammensetzen.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Erzeugen Sie zunächst den Kopf der Funktion für ein einzelnes Kuchenstück. Überlegen Sie anschließend, wie Sie das Dreieck zeichnen könnten. Welche Informationen müssen dem Kopf der Funktion übergeben werden?\n",
    "      \n",
    "   </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Die Funktion für das Kuchenstück muss die Schildkröte, die Seitenlänge (die der Radius der Form \"Kuchen ist, daher nennen wir sie \"r\") und den Winkel übergeben bekommen, in dem das Kuchenstück gezeichnet werden soll. \n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Da wir die beiden Seitenlängen vorgeben, müssen wir die obere Länge in Abhängigkeit von den Seitenlängen (dem Radius der Form Kuchen und dem Winkel berechnen. Wir verwenden das sogenannte Bogenmaß. Die vollständige dafür Formel ist $2*r*sin(angle*\\pi/180)$   \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Um Herauszufinden, wie weit sich die Schildkröte drehen muss, ist es am Einfachsten verschiedene Drehwinkel auszuprobieren, bis es funktioniert. Verwenden Sie 90 Winkel als Basis und addieren oder subtrahieren Sie den Winkel aus dem Funktionskopf\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Damit die Schildkröte den gesamten Kuchen zeichnen kann muss Sie immer in derselben Position starten und enden. Dafür muss Sie sich zu Beginn im angegebenen Winkel drehen und am Ende soweit, dass sie wieder die Ausgangsposition annimmt. Um die Position wieder anzunehmen muss sich die Schildkröte um weniger als 180 Grad drehen. Der genaue Winkel kann mit Hilfe des Winkel-Parameters berechnet werden. \n",
    "  \n",
    "   </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">7. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Um die Kuchen-Funktion zu schreiben können Sie die Blume-Funktion kopieren und anpassen. Es müssen einige Veränderungen vorgenommen werden. Überlegen Sie welche Änderungen das sind. Um einen Eindruck zu bekommen, können Sie Kuchen aufrufen und sehen welche Fehler auftreten.\n",
    "\n",
    " </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">8. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Damit der Kuchen ohne Lücken gezeichnet werden kann muss der Winkel berechnet werden und nicht der Funktion übergeben werden. Im Funktionskopf muss also nur der Radius der Figur, also die Seitenlänge der einzelnen Stücke, die Schildkröte und die Anzahl der Stücke übergeben werden. Der Winkel wird dann in Abhängigkeit von der Anzahl der Stücke berechnet.\n",
    "\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">9. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "\n",
    "Der Winkel zwischen den Stücken ist, da wir eine volle Drehung vornehmen wollen 360 geteilt durch die Anzahl der Stücke. In der Schleife rufen wir Stück auf, dort müssen wir den Winkel anpassen, bevor wir die entsprechende Drehung vornehmen. Führen Sie die Funktion aus und versuchen Sie herauszufinden, wie Sie den Winkel in stück anpassen müssen.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">10. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Der Winkel für Stück ist der halbe Winkel zwischen Stücken. Wir nehmen also die Winkelvariable/2 als zu übergebenden Wert.\n",
    "\n",
    "   </div>       \n",
    "</details>\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "\n",
    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
    "\n",
    "(Quelle: Jason Eppink, Flickr)\n",
    "\n",
    "*(Hier ist eine mögliche [Lösung](http://thinkpython2.com/code/pie.py))*"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import math\n",
    "import turtle\n",
    "\n",
    "# Arbeiten Sie diese Lösung durch und kommentieren Sie die einzelnen Schritte\n",
    "\n",
    "def stück (t,r, angle):\n",
    "    c=2*r*(math.sin(angle*math.pi/180))\n",
    "    t.rt(angle)\n",
    "    t.fd(r)\n",
    "    t.lt(90+angle)\n",
    "    t.fd(c)\n",
    "    t.lt(90+angle)\n",
    "    t.fd(r)\n",
    "    t.lt(180-angle)\n",
    "\n",
    "\n",
    "def kuchen (t, n, r):\n",
    "    angle=360/n\n",
    "    for i in range (n):\n",
    "        stück(t,r,angle/2)\n",
    "        t.lt(angle)\n",
    "    turtle.mainloop()\n",
    "    turtle.bye()\n",
    "    \n",
    "    \n",
    "bob=turtle.Turtle()  \n",
    "kuchen(bob, 5, 100)\n",
    "\n",
    "turtle.mainloop() \n",
    "turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Aufgabe 4\n",
    "\n",
    "\n",
    "Lesen Sie etwas zu Spiralen auf [Wikipedia](https://de.wikipedia.org/wiki/Spirale). Schreiben Sie dann ein Programm, welches eine [Archimedische Spirale](https://de.wikipedia.org/wiki/Archimedische_Spirale) (oder eine andere) zeichnet.\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">1. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "In dieser Aufgabe, können Sie entscheiden, wie komplex Sie die Schnittstelle gestalten wollen. Sie müssen mindestens die Schildkröte übergeben, die die Spirale zeichnen soll, in maximaler Komplexität kann der Nutzer alle Variablen der Spirale anpassen. Hier wurde entschieden, dass der Nutzer lediglich die Schildkröte und die Anzahl der Spiralensegmente angeben darf, wenn Sie eine komplexere Lösung haben wollen, fügen Sie diese Parameter dem Funktionsaufruf hinzu.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">2. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Die Formel für die Berechnung von Spiralen ist $r = a + b*\\theta$. Dabei können Sie einfach Ausgangswerte für a und b festlegen. Ein geeigneter Wert für a ist zum Beispiel 0.1 und für b 0.0002. Wenn ihre Funktion funktioniert, probieren Sie verschiedene Werte für a und b aus und sehen Sie sich an, wie die Spirale sich verändert.      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">3. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Weitere Parameter können entweder in der Schnittstelle oder aber wie in dem Beispiel unten in der Funktion festgelegt werden. Diese Parameter sind der Ausgangswinkel theta der Spirale und die Länge der einzelnen Spiralensegmente.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">4. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Analog zum Kreisbogen wird auch die Spirale durch kurze gerade Segmente und Drehungen gezeichnet. Da das Zeichnen von Segmenten n-mal wiederholt wird, benötigen Sie eine for-Schleife.\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">5. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "In der Schleife muss für jedes Segment neu berechnet werden wie weit die Schildkröte sich drehen muss, da der Winkel nicht konstant bleibt. Dafür verwendet die Lösung: dtheta = 1 / (a + b * theta)\n",
    "      \n",
    "  </div>       \n",
    "</details>\n",
    "\n",
    "\n",
    "<details>\n",
    "    <summary type=\"button\" class=\"btn btn-primary\">6. Hinweis</summary>\n",
    "  <div class=\"alert alert-info\" role=\"alert\">\n",
    "      \n",
    "Da diese Formel theta als den Winkel des vorherigen Abschnitts verwendet, muss theta ebenfalls in jedem Schleifendurchlauf überschrieben werden - also addieren Sie dtheta auf theta auf. \n",
    "       \n",
    "  </div>       \n",
    "</details>\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<a data-flickr-embed=\"true\"  href=\"https://www.flickr.com/photos/jasoneppink/4964471335\" title=\"Spoiler Alert\"><img src=\"https://farm5.staticflickr.com/4110/4964471335_1f86a923f3_n.jpg\" width=\"320\" height=\"213\" alt=\"Spoiler Alert\"></a><script async src=\"//embedr.flickr.com/assets/client-code.js\" charset=\"utf-8\"></script>\n",
    "\n",
    "\n",
    "Eine [Lösung](http://thinkpython2.com/code/spiral.py)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def spirale(t,n):\n",
    "    '''In dieser Spirale bestimmt der Nutzer, wie viele Segmente gezeichnet werden, die Windung der Spirale ist\n",
    "    in der Funktion festgelegt.\n",
    "    '''\n",
    "    length=3 \n",
    "    a=0.1\n",
    "    b=0.0002\n",
    "    theta=0.0\n",
    "    for i in range (n):\n",
    "        t.fd(length)\n",
    "        dtheta = 1 / (a + b * theta)\n",
    "        t.lt(dtheta)\n",
    "        theta = theta + dtheta\n",
    "\n",
    "import turtle\n",
    "bob=turtle.Turtle()        \n",
    "spirale(bob,1000)\n",
    "turtle.mainloop()\n",
    "turtle.bye()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "\n",
    "### Aufgabe 5\n",
    "\n",
    "*(Hinweis: Dies ist eher eine Fleiß- und Zusatzaufgabe.)*\n",
    "\n",
    "Die Buchstaben des Alphabets sind aus ein paar grundlegenden Elementen zusammengesetzt wie z.B. vertikalen und horizontalen Linien und einigen Kurven. Entwerfen Sie ein Alphabet, welches mit einer kleinen Anzahl einfacher Elemente gezeichnet werden kann und schreiben Sie dann Funktionen zum Zeichnen der Buchstaben. \n",
    "\n",
    "Sie sollten eine Funktion für jeden Buchstaben schreiben, die Sie `draw_a`, `draw_b`, etc. nennen und diese Funktionen in eine Datei namens `letters.py` packen. Sie können [hier](http://thinkpython2.com/code/typewriter.py) eine \"Schildkrötenschreibmaschine\" herunterladen und damit ihren Code testen.\n",
    "\n",
    "\n",
    "Das könnte dann so aussehen:\n",
    "![Schreibmaschine](https://box.hu-berlin.de/f/fec51b18a8af4535b445/?dl=1)\n",
    "\n",
    "Sie finden eine Lösung für diese Aufgabe [hier](http://thinkpython2.com/code/letters.py); Diese benötigt auch [polygon.py](http://thinkpython2.com/code/polygon.py)."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "![Speichern](https://amor.cms.hu-berlin.de/~jaeschkr/teaching/spp/floppy.png) Speichern Sie dieses Notebook, so dass Ihre Änderungen nicht verlorengehen (nicht auf einem Pool-Rechner). Klicken Sie dazu oben links auf das Disketten-Icon und nutzen Sie beispielsweise einen USB-Stick, E-Mail, Google Drive, Dropbox oder Ihre [HU-Box](https://box.hu-berlin.de/).  "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "![Smiley](https://upload.wikimedia.org/wikipedia/commons/8/85/Smiley.svg)\n",
    "\n",
    "Herzlichen Glückwunsch! Sie haben das 4. Kapitel geschafft. Weiter geht es in [5: Bedingungen und Rekursion](seminar05.ipynb)."
   ]
  }
 ],
 "metadata": {
  "language_info": {
   "name": "python",
   "pygments_lexer": "ipython3"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}